На этом шаге мы рассмотрим структуру тестовых данных.
В нашей версии задачи коммивояжер заинтересован в посещении пяти крупных городов штата Вермонт. Мы не будем указывать начальный (а следовательно, конечный) город. На рисунке 1 показаны пять городов и расстояния между ними.
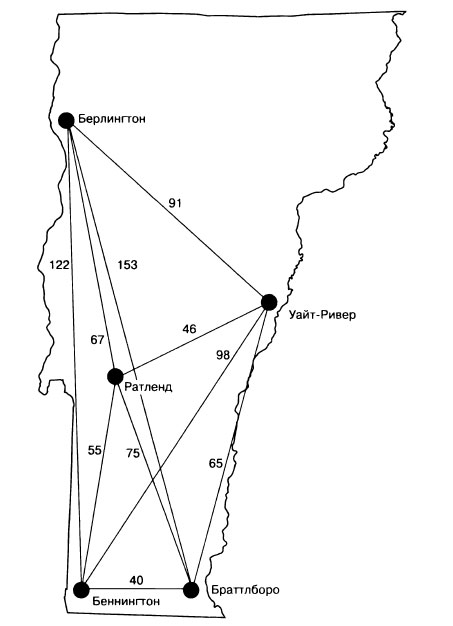
Рис.1. Пять городов штата Вермонт и рассrояния между ними
Обратите внимание на то, что для построения маршрута указано расстояние между каждой парой городов.
Возможно, вам уже встречались таблицы расстояний. В них можно легко найти расстояние между любыми двумя городами. В таблице 1 перечислены расстояния для пяти городов, используемых в задаче.
| Город | Ратленд | Берлингтон | Уайт-Ривер | Беннингтон | Браттлборо |
|---|---|---|---|---|---|
| Ратленд | 0 | 67 | 46 | 55 | 75 |
| Берлингтон | 67 | 0 | 91 | 122 | 153 |
| Уайт-Ривер | 46 | 91 | 0 | 98 | 65 |
| Беннингтон | 55 | 122 | 98 | 0 | 40 |
| Браттлборо | 75 | 153 | 65 | 40 | 0 |
Для решения задачи нужно кодифицировать города и расстояния между ними. Чтобы облегчить поиск расстояний между городами, мы будем использовать словарь словарей с множеством внешних ключей, представляющих первый город пары, и множеством внутренних ключей, представляющих ее второй город. Это будет тип Dict[str, Dict[str, int]], и он будет допускать поиск типа vt_distances["Ратленд"] ["Берлингтон"], который должен возвращать 67.
from typing import Dict, List, Iterable, Tuple from itertools import permutations vt_distances: Dict[str, Dict[str, int]] = { "Ратленд": {"Берлингтон": 67, "Уайт-Ривер": 46, "Беннингтон": 55, "Браттлборо": 75}, "Берлингтон": {"Ратленд": 67, "Уайт-Ривер": 91, "Беннингтон": 122, "Браттлборо": 153}, "Уайт-Ривер": {"Ратленд": 46, "Берлингтон": 91, "Беннингтон": 98, "Браттлборо": 65}, "Беннингтон": {"Ратленд": 55, "Берлингтон": 122, "Уайт-Ривер": 98, "Браттлборо": 40}, "Браттлборо": {"Ратленд": 75, "Берлингтон": 153, "Уайт-Ривер": 65, "Беннингтон": 40} }
На следующем шаге мы рассмотрим перебор всех вариантов.
