На этом шаге мы рассмотрим дадим их краткую характеристику.
Хотя первый успех нейронных сетей в 1990-х и привлек к ним внимание исследователей, новый разработанный подход к машинному обучению - ядерные методы (kernel methods) - быстро отправил нейронные сети обратно в небытие . Ядерные методы - это группа алгоритмов классификации, из которых наибольшую известность получил метод опорных векторов (Support Vector Machine, SVM). Современная формулировка SVM была предложена Владимиром Вапником и Коринной Кортес в начале 1990-х в Bell Labs и опубликована в 1995 году,
Vapnik V., Cortes C. Support-Vector Networks // Machine Learning 20, no. 3 (1995): 273–297.
хотя прежняя линейная формулировка была обнародована Вапником и Алексеем Червоненкисом еще в 1963 году.
Vapnik V., Chervonenkis A. A Note on One Class of Perceptrons // Automation and Remote Control 25 (1964).
Метод опорных векторов - это алгоритм классификации, предназначенный для поиска хороших "решающих границ", разделяющих два класса (рисунок 1).
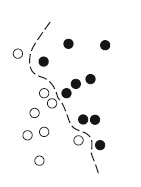
Рис.1. Решающая граница
Он выполняется в два этапа.
- Данные отображаются в новое пространство более высокой размерности, где граница может быть представлена как гиперплоскость (если данные были двумерными, как на рисунке 1, гиперплоскость вырождается в линию).
- Хорошая решающая граница (разделяющая гиперплоскость) вычисляется путем максимизации расстояния от гиперплоскости до ближайших точек каждого класса. Этот этап называют максимизацией зазора. Он позволяет обобщить классификацию новых образцов, не принадлежащих обучающему набору данных.
Методика отображения данных в пространство более высокой размерности, где задача классификации становится проще, может хорошо выглядеть на бумаге, но на практике часто оказывается трудноразрешимой. Вот тут и приходит на помощь изящная процедура kernel trick (ключевая идея, по которой ядерные методы получили свое название). Суть ее заключается в следующем: чтобы найти хорошие решающие гиперплоскости в новом пространстве, явно определять координаты точек в этом пространстве не требуется; достаточно вычислить расстояния между парами точек - эффективно это можно сделать с помощью функции ядра. Функция ядра - это незатратная вычислительная операция, отображающая любые две точки из исходного пространства и вычисляющая расстояние между ними в целевом пространстве представления, полностью минуя явное вычисление нового представления. Функции ядра обычно определяются вручную, а не извлекаются из данных - в случае с методом опорных векторов по данным определяется только разделяющая гиперплоскость.
На момент разработки метод опорных векторов демонстрировал лучшую производительность на простых задачах классификации и был одним из немногих методов машинного обучения, обладающих обширной теоретической базой и поддающихся серьезному математическому анализу, что сделало его понятным и легко интерпретируемым. Благодаря этому SVM приобрел чрезвычайную популярность на долгие годы. Однако он оказался трудноприменимым к большим наборам данных и не давал хороших результатов для таких задач, как классификация изображений. Поскольку метод опорных векторов является поверхностным методом, для его использования в распознавании данных требуется сначала вручную определить представительную выборку (этот шаг называется конструированием признаков), что сопряжено со сложностями и чревато ошибками. Например, у вас не получится применить SVM для классификации рукописных цифр, имея только исходные изображения; вам придется сначала вручную найти такие представления изображений, которые упростят решение задачи, например вышеупомянутые гистограммы распределения пикселей.
На следующем шаге мы рассмотрим деревья решений, случайные леса и градиентный бустинг.
