На этом шаге мы закончим построение линейного классификатора.
Давайте создадим переменные W и b, инициализированные случайными значениями и нулями соответственно.
Пример 3.17. Создание переменных для линейного классификатора
import tensorflow as tf input_dim = 2 # На вход подаются двумерные точки # Прогноз на выходе - единственная оценка для каждого образца (близкая к 0, # если предполагается, что образец относится к классу 0, или к 1, если предполагается, # что образец относится к классу 1) output_dim = 1 W = tf.Variable(initial_value=tf.random.uniform(shape=(input_dim, output_dim))) b = tf.Variable(initial_value=tf.zeros(shape=(output_dim,)))
Вот функция прямого прохода.
Пример 3.18. Функция прямого прохода
def model(inputs): return tf.matmul(inputs, W) + b
Наш линейный классификатор будет работать с двумерными входными данными, поэтому W на самом деле представляет два скалярных коэффициента, w1 и w2: W = [[w1], [w2]], а b - единственный скалярный коэффициент. То есть прогноз для каждой данной входной точки [x, y] вычисляется так:
prediction = [w1], [w2]] · [x, y] + b = w1 * x + w2 * y + b.
В следующем примере показана наша функция потерь .
Пример 3.19. Функция потерь, вычисляющая средний квадрат ошибок
def square_loss(targets, predictions): # Тензор per_sample_losses имеет ту же форму, что и тензоры # targets и predictions, и содержит оценки потерь для каждого образца per_sample_losses = tf.square(targets - predictions) # Нам нужно усреднить оценки потерь по образцам в одно скалярное # значение потерь: именно это делает reduce_mean return tf.reduce_mean(per_sample_losses)
Далее следует этап обучения, который принимает некоторые обучающие данные и обновляет веса W и b, стремясь минимизировать потери на данных.
Пример 3.20. Функция этапа обучения
learning_rate = 0.1 def training_step(inputs, targets): with tf.GradientTape() as tape: # Прямой проход внутри контекста GradientTape predictions = model(inputs) loss = square_loss(predictions, targets) # Получение градиента потерь относительно весов grad_loss_wrt_W, grad_loss_wrt_b = tape.gradient(loss, [W, b]) # Обновление весов W.assign_sub(grad_loss_wrt_W * learning_rate) b.assign_sub(grad_loss_wrt_b * learning_rate) return loss
Для простоты используем пакетное обучение вместо мини-пакетного: будем запускать каждый шаг обучения (вычисление градиента и обновление весов) сразу для всех данных, не перебирая их небольшими партиями. С одной стороны, это означает, что каждый шаг обучения будет занимать гораздо больше времени, поскольку прямой проход и вычисление градиентов будут производиться для 2000 образцов одновременно. С другой стороны, с каждым новым обновлением градиента потери на обучающих данных будут снижаться намного эффективнее, ведь в расчетах будут участвовать сразу все образцы, а не, скажем, 128 случайно отобранных. В результате потребуется намного меньше шагов обучения и можно взять более высокую скорость обучения, чем при обычном обучении на небольших пакетах (мы используем learning_rate = 0.1, как определено в примере 3.20) .
Пример 3.21. Цикл пакетного обучения
for step in range(40): loss = training_step(inputs, targets) print(f"Loss at step {step}: {loss:.4f}") Loss at step 0: 1.3776 Loss at step 1: 0.2719 Loss at step 2: 0.1318 Loss at step 3: 0.1078 Loss at step 4: 0.0985 Loss at step 5: 0.0916 Loss at step 6: 0.0855 Loss at step 7: 0.0800 Loss at step 8: 0.0750 Loss at step 9: 0.0705 Loss at step 10: 0.0663 Loss at step 11: 0.0625 Loss at step 12: 0.0591 Loss at step 13: 0.0560 Loss at step 14: 0.0532 Loss at step 15: 0.0506 Loss at step 16: 0.0482 Loss at step 17: 0.0461 Loss at step 18: 0.0442 Loss at step 19: 0.0424 Loss at step 20: 0.0408 Loss at step 21: 0.0393 Loss at step 22: 0.0380 Loss at step 23: 0.0368 Loss at step 24: 0.0357 Loss at step 25: 0.0347 Loss at step 26: 0.0338 Loss at step 27: 0.0330 Loss at step 28: 0.0322 Loss at step 29: 0.0315 Loss at step 30: 0.0309 Loss at step 31: 0.0303 Loss at step 32: 0.0298 Loss at step 33: 0.0294 Loss at step 34: 0.0289 Loss at step 35: 0.0286 Loss at step 36: 0.0282 Loss at step 37: 0.0279 Loss at step 38: 0.0276 Loss at step 39: 0.0273
После 40 циклов обучения величина потерь стабилизировалась на уровне около 0,027. Посмотрим, как получившаяся линейная модель классифицирует точки из обучающего набора данных. Поскольку целевыми значениями у нас служат нули и единицы, всякая входная точка будет классифицироваться как 0, если прогнозируемое значение для нее ниже 0,5, и как 1, если больше 0,5 (рисунок 1).
predictions = model(inputs) plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5) plt.show()
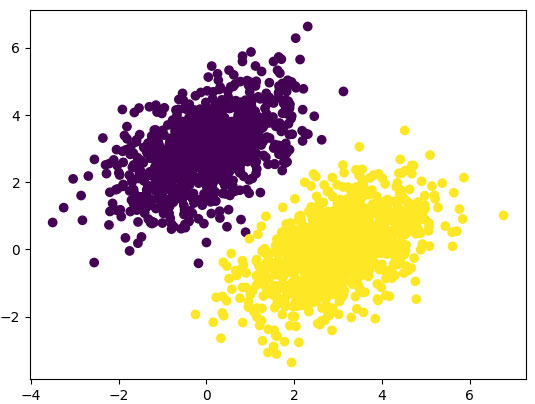
Рис.1. Прогноз нашей модели очень близок к исходной картине
Напомним, что значение прогноза для данной точки [x, у] вычисляется как
prediction = [[w1], [w2]] · [x, у] + b = w1 * x + w2 * у + b .
Построим эту линию (рисунок 2):
# Сгенерировать 100 чисел, равномерно распределенных в интервале от -1 до 4, # которые будут использоваться для рисования прямой x = np.linspace(-1, 4, 100) y = - W[0] / W[1] * x + (0.5 - b) / W[1] # Это уравнение нашей прямой plt.plot(x, y, "-r") # Нарисовать линию ("-r" означает красный (red) цвет) # Тут же нарисовать прогноз нашей модели plt.scatter(inputs[:, 0], inputs[:, 1], c=predictions[:, 0] > 0.5)
Блокнот с приведенными на этом шаге примерами можно взять здесь.
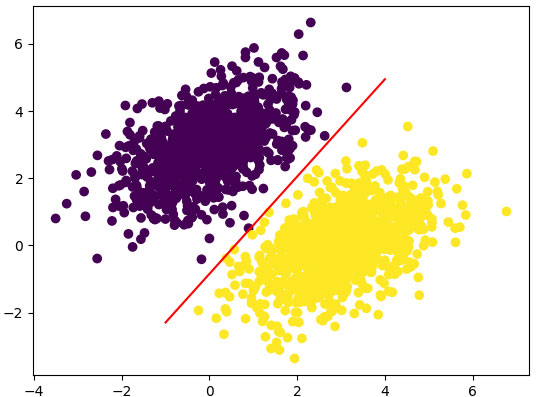
Рис.2. Наша модель изображена как прямая линия
В этом и заключается суть линейного классификатора: поиск параметров линии (или, в многомерных пространствах, гиперплоскости), аккуратно разделяющей два класса данных.
На следующем шаге мы начнем знакомиться с основами Keras.
