На этом шаге мы закончим изучение этого вопроса.
Повторим уже знакомые нам действия. Выходной результат 60 все еще слишком мал. Давайте вновь немного изменим константу с, увеличив ее значение с 0,6 до 0,7.
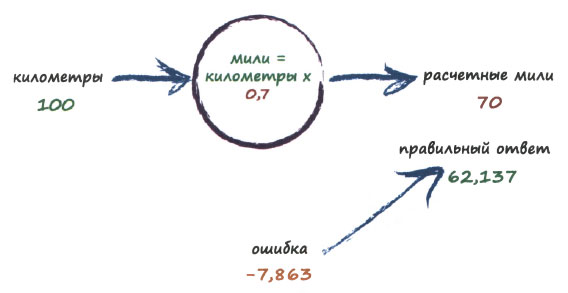
О, нет! Мы перестарались и получили результат, превышающий правильный ответ. Предыдущая ошибка была равна 2,137, а теперь она составляет -7,683. Знак "минус" просто свидетельствует о том, что вместо недооценки истинного результата произошла его переоценка (напомню, что величина ошибки определяется выражением правильное значение минус расчетное значение).
Итак, с=0,6 было гораздо лучше, чем с=0,7. Сейчас мы могли бы признать величину ошибки при с=0,6 удовлетворительной и закончить это упражнение. Но мы все-таки продвинемся еще чуть дальше. Почему бы нам не попытаться ввести очень малую поправку и увеличить значение с с 0,6 до, скажем, 0,61?
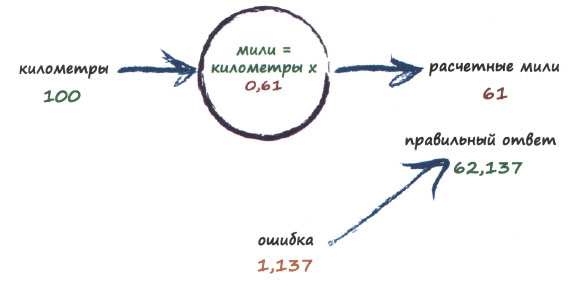
Это дает нам гораздо лучший результат, чем предыдущие, поскольку теперь выходное значение 61 отличается от правильного значения 62,137 всего лишь на 1,137.
Итак, последняя попытка научила нас тому, что величину поправки к величине с необходимо каждый раз определять заново. Если выходной результат приближается к правильному ответу, т.е. если ошибка уменьшается, то не следует оставлять величину поправки прежней. Тем самым мы избегаем переоценки значения по сравнению с истинным, как это было ранее.
Опять-таки, не отвлекаясь на поиск точных способов определения величины с и по-прежнему фокусируя внимание на идее ее постепенного уточнения, мы можем предположить, что поправка должна выражаться некоторой долей ошибки. Это интуитивно понятно: большая ошибка указывает на необходимость введения большей поправки, тогда как малая ошибка нуждается в незначительной поправке.
Хотите - верьте, хотите - нет, но то, что мы сейчас сделали, передает суть процесса обучения нейронной сети. Мы тренировали машину так, чтобы ее предсказания становились все более и более точными.
Нам стоит сделать небольшую паузу, чтобы поразмышлять над следующим: мы не находили точного решения задачи в один прием, как это часто делается при решении школьных или научных задач. Вместо этого мы предприняли совершенно иной подход, заключающийся в многократных попытках проверки пробного значения и его уточнения. Такие процессы иногда называют итеративными, что как раз и означает постепенное, шаг за шагом, улучшение искомого результата.
Резюме
- У всех полезных компьютерных систем имеются каналы ввода и вывода, между которыми над данными выполняются некоторые вычисления. В случае нейронных сетей это не так.
- Если точные принципы функционирования какой-либо системы нам неизвестны, то мы пытаемся получить представление о том, как она работает, используя модель с регулируемыми параметрами. Если бы мы не знали, как преобразовать километры в мили, то могли бы использовать для этой цели линейную функцию в качестве модели с регулируемым наклоном.
- Неплохим способом улучшения подобных моделей является настройка параметров на основании сравнения результатов модели с точными результатами в известных примерах.
На следующем шаге мы сравним задачи классификации и прогнозирования.
