На этом шаге мы продолжим тренировку.

Ранее было показано, что параметр А управляет наклоном линии. Чем больше А, тем больше крутизна наклона.

Для начала примем, что А=0,25. Тогда разделительная линия описывается уравнением

     у=0,25х                    .

Отобразим эту линию в графическом виде на той же диаграмме, на которой отложены тренировочные данные.

Благодаря графику мы безо всяких вычислений сразу же видим, что линия у=0,25х не является хорошим классификатором. Она не отделяет один тип жуков от другого. Например, мы не можем делать утверждения наподобие "Если точка данных располагается над линией, то она соответствует гусенице", поскольку точно там же располагаются и данные божьей коровки.

Интуитивно мы понимаем, что правый край линии следует немного приподнять. Мы устоим перед соблазном сделать это, глядя на диаграмму и проводя подходящую линию вручную. Мы хотим проверить, не удастся ли нам подобрать для этого подходящий повторяемый рецепт, последовательность команд, которую компьютерщики называют алгоритмом.

Обратимся к первому тренировочному примеру, соответствующему божьей коровке: ширина - 3,0 и длина - 1,0. Если бы мы тестировали функцию у=Ах с этим примером, в котором х равен 3,0, то получили бы следующий результат:

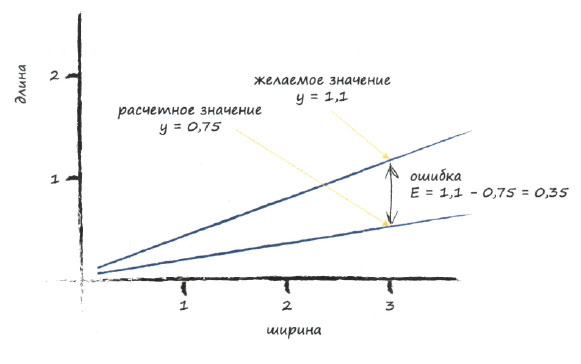
        у= (0,25) * (3,0) = 0,75

Функция, в которой для параметра А установлено начальное случайно выбранное значение, равное 0,25, сообщает, что для жука шириной 3,0 длина должна быть равна 0,75. Мы знаем, что это слишком мало, поскольку согласно тренировочным данным длина жука равна 1,0.

Итак, налицо расхождение, или ошибка. Точно так же, как в примере с предиктором, преобразующим километры в мили, мы можем использовать величину этой ошибки для получения информации о том, каким образом следует корректировать параметр А.

Однако сначала давайте подумаем, каким должно быть значение у. Если положить его равным 1,0, то линия пройдет через точку с координатами

      (х, у) = (3,0; 1,0),

соответствующую божьей коровке. Само по себе это неплохо, но это не совсем то, что нам нужно. Нам желательно, чтобы линия проходила над этой точкой. Почему? Да потому, что мы хотим, чтобы точки данных божьей коровки лежали под линией, а не на ней. Линия должна служить разделителем между точками данных божьих коровок и гусениц, а не предсказывать длину жука по известной ширине.

В связи с этим попробуем нацелиться на значение у=1,1 при х=3,0. Оно лишь ненамного больше 1,0. Вместо него можно было бы взять значение 1,2 или 1,3, но никак не 10 или 100, поскольку с большой долей вероятности это привет к тому, что прямая будет проходить над всеми точками данных, как божьих коровок, так и гусениц, в результате чего она станет полностью бесполезной в качестве разделителя.

Следовательно, мы выбираем целевое значение 1,1 и определяем ошибку Е с помощью следующей формулы:

     ошибка = желаемое целевое значение - фактический результат

Или (после подстановки значений):

     Е = 1,1 - 0,75 = 0,35

Помня о пользе визуализации информации, обратимся к приведенной ниже диаграмме, на которой в графическом виде представлены ошибка, а также целевое и расчетное значения.

Вы спросите: а каким образом наше знание величины ошибки Е может помочь в нахождении лучшего значения для параметра А? Это очень важный вопрос.

На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг