На этом шаге мы напомним правило умножения матриц.
Матрицы пользуются ужасной репутацией. Они вызывают воспоминания о тех долгих и утомительных часах, которые в студенческие годы приходилось тратить на, казалось бы, совершенно бесцельное и никому не нужное занятие - перемножение матриц.
Перед этим мы вручную выполнили вычисления для двухслойной сети, содержащей всего лишь по 2 узла в каждом слое. Однако даже в этом случае объем работы оказался довольно большим, а что тогда можно сказать, например, о сети, состоящей из пяти слоев по 100 узлов? Уже сама по себе запись всех необходимых выражений была бы сложной задачей. Составление комбинаций сигналов, умножение на подходящие весовые коэффициенты, применение сигмоиды для каждого узла... Ух!
Так чем же нам могут помочь матрицы? Они будут нам полезны в двух отношениях. Во-первых, они обеспечивают сжатую запись операций, придавая им чрезвычайно компактную форму. Это большой плюс для нас, поскольку такая работа утомительна, требует концентрации внимания и чревата ошибками. Во-вторых, в большинстве компьютерных языков программирования предусмотрена работа с матрицами, а поскольку многие операции при этом повторяются, компьютеры распознают это и выполняют их очень быстро.
Резюмируя, можно сказать, что матрицы позволяют формулировать задачи в более простой и компактной форме и обеспечивают их более быстрое и эффективное выполнение.
Теперь, когда вам известны причины, по которым мы собираемся воспользоваться матрицами несмотря на возможный горький опыт знакомства с ними в студенческие годы, давайте демистифицируем матрицы, начав работать с ними.
Матрица - это всего лишь таблица, прямоугольная сетка, образованная числами. Вот и все. Все, что связано с матрицами, ничуть не сложнее этого.
Если вы уже пользовались электронными таблицами, то никаких сложностей при работе с числами, располагающимися в ячейках сетки, у вас возникнуть не должно. Ниже показан пример рабочего листа Excel с числовой таблицей.

Это и есть матрица - таблица или сетка, образованная числами, точно так же, как и следующий пример матрицы размером 2x3.

При обозначении матриц принято указывать сначала количество строк, а затем количество столбцов. Поэтому размерность данной матрицы не 3x2, а 2x3.
Кроме того, иногда матрицы заключают в квадратные скобки, иногда - в круглые, как это сделали мы.
На самом деле матрицы не обязательно должны состоять из чисел. Они могут включать величины, которым мы дали имена, но не присвоили фактических значений. Поэтому на следующей иллюстрации также показана матрица с элементами в виде переменных, каждая из которых имеет определенный смысл и может иметь значение, просто мы пока не указали, что это за значения.

Чем полезны матрицы, вам станет понятно, когда мы рассмотрим, как они умножаются. Возможно, вы это помните еще из курса высшей математики, а если нет, то освежите свою память.
Вот пример умножения одной простой матрицы на другую.
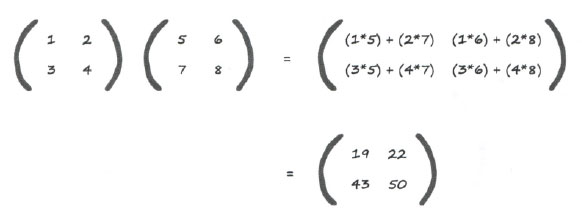
Как видите, эта операция не сводится к простому перемножению соответствующих элементов. Левый верхний элемент не равен 1*5, как и правый нижний - не 4*8.
Вместо этого матрицы умножаются по другим правилам. Возможно, вы и сами догадаетесь, по каким именно, если внимательно присмотритесь к примеру. Если нет, то взгляните на приведенную ниже иллюстрацию, где показано, как получается ответ для левого верхнего элемента.
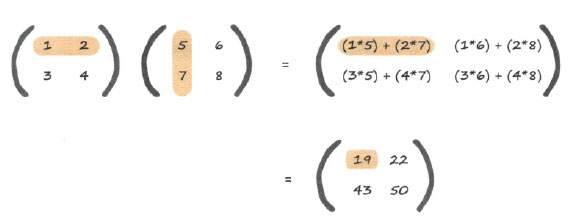
Вы видите, что верхний левый элемент вычисляется с использованием верхней строки первой матрицы и левого столбца второй. Мысленно перебирая обе последовательности элементов, перемножьте их попарно и сложите полученные результаты. Таким образом, чтобы вычислить левый верхний элемент результирующей матрицы, мы начинаем перемещаться вдоль верхней строки первой матрицы, где находим число 1, а начиная перемещение вниз по левому столбцу второй матрицы, находим число 5. Мы перемножаем их и запоминаем результат, который равен 5. Мы продолжаем перемещаться вдоль ряда и вниз по столбцу и находим элементы 2 и 7. Результат их перемножения, равный 14, мы также запоминаем. При этом мы уже достигли конца строки и столбца, поэтому суммируем числа, которые перед этим запомнили, и получаем в качестве результата число 19. Это и есть левый верхний элемент результирующей матрицы.
Описание получилось длинным, но выполнение самих действий не отнимает много времени. Продолжите далее самостоятельно. На приведенной ниже иллюстрации показано, как вычисляется правый нижний элемент результирующей матрицы.

Вы вновь можете видеть, как, используя строку и столбец, которые соответствуют искомому элементу (в данном случае вторая строка и второй столбец), мы получаем два произведения, и сложение которых дает 18 + 32 = 50.
Продолжая действовать в таком же духе, находим, что левый нижний элемент равен (3*5) + (4*7) = 15 + 28 = 43, а правый верхний - (1*6) + (2*8) = 6 + 16 = 22.
На следующей иллюстрации продемонстрировано использование переменных вместо чисел:
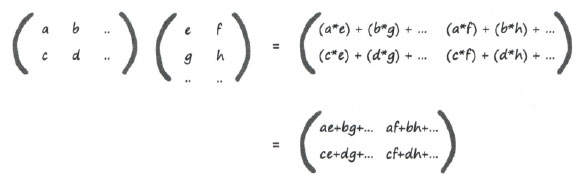
Это всего лишь другой способ описания подхода, с помощью которого мы умножаем матрицы. Используя буквы, вместо которых могут быть подставлены любые числа, мы даем общее описание этого подхода. Такое описание действительно является более общим, чем предыдущее, поскольку применимо к матрицам различных размеров.
Говоря о применимости описанного подхода к матрицам любого размера, следует сделать одну важную оговорку: умножаемые матрицы должны быть совместимыми. Вы поймете, в чем здесь дело, вспомнив, как отбирали попарно элементы из строк первой матрицы и столбцов второй: этот метод не сможет работать, если количество элементов в строке не будет совпадать с количеством элементов в столбце. Поэтому вы не сможете умножить матрицу 2x2 на матрицу 5x5. Попытайтесь это сделать, и сами увидите, почему это невозможно. Чтобы матрицы можно было умножить, количество столбцов в первой из них должно совпадать с количеством строк во второй.
В разных руководствах этот тип матричного умножения может встречаться под разными названиями: скалярное произведение, точечное произведение или внутреннее произведение. В математике возможны и другие типы умножения матриц, такие как перекрестное произведение, но мы будем работать с точечным произведением матриц.
Но почему мы должны углубляться в дебри этого ужасного матричного умножения и отвратительной алгебры? На то есть серьезная причина... Крепитесь!
На следующем шаге мы закончим изучение этого вопроса.
