На этом шаге мы рассмотрим способ задания весовых коэффициентов.
Итак, нашим следующим шагом будет создание сети, состоящей из узлов и связей. Наиболее важная часть этой сети - весовые коэффициенты связей (веса). Они используются для расчета распространения сигналов в прямом направлении, а также обратного распространения ошибок, и именно весовые коэффициенты уточняются в попытке улучшить характеристики сети.
Ранее вы уже видели, насколько удобна компактная запись весов в виде матриц. Следовательно, мы можем создать следующие матрицы:
- матрицу весов для связей между входным и скрытым слоями, wвходной_скрытый, размерностью hidden_nodes * input_nodes;
- другую матрицу для связей между скрытым и выходным слоями, wскрытый_выходной, размерностью output_nodes * hidden_nodes.
При необходимости вернитесь к шагам, где излагается теоретический материал, чтобы понять, почему первая матрица имеет размерность hidden_nodes * input_nodes, а не input_nodes * hidden_nodes.
Вспомните, что начальные значения весовых коэффициентов должны быть небольшими и выбираться случайным образом. Следующая функция из пакета numpy генерирует массив случайных чисел в диапазоне от 0 до 1, где размерность массива равна rows * columns:
numpy.random.rand(rows, columns)
Все хорошие программисты ищут в Интернете онлайновую документацию по функциям Python и даже находят полезные функции, о существовании которых и не подозревали. Выполните такой поиск для функции numpy.random, rand(), если хотите узнать о ней больше.
Если мы собираемся использовать расширения пакета numpy, мы должны импортировать эту библиотеку в самом начете кода. Прежде всего удостоверимся, что нужная нам функция работает. В приведенном ниже примере используется матрица размерностью 3*3. Как видите, матрица заполнилась случайными значениями в диапазоне от 0 до 1.
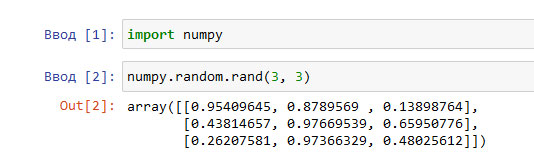
Рис.1. Заполнение матрицы случайными числами
Данный подход можно улучшить, поскольку весовые коэффициенты могут иметь не только положительные, но и отрицательные значения и изменяться в пределах от -1,0 до +1,0. Для простоты мы вычтем 0,5 из этих граничных значений, перейдя к диапазону значений от -0,5 до +0,5. Ниже представлены результаты применения этого изящного подхода, которые демонстрируют, что некоторые весовые коэффициенты теперь имеют отрицательные значения.
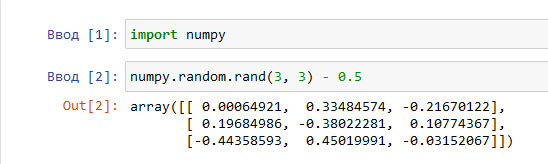
Рис.2. Результат изменения диапазона
Мы готовы создать матрицу начальных весов в нашей программе на Python. Эти весовые коэффициенты составляют неотъемлемую часть нейронной сети и служат ее характеристиками на протяжении всей ее жизни, а не временным набором данных, которые исчезают сразу же после того, как функция отработала. Это означает, что они должны быть частью процесса инициализации и быть доступными для других методов, таких как функции тренировки и опроса сети.
Ниже приведен код, включая комментарии, который создает две матрицы весовых коэффициентов, используя значения переменных self.inodes, self.hnodes и self.onodes для задания соответствующих размеров каждой из них.
# Матрицы весовых коэффициентов связей wih (между входным и скрытым # слоями) и who (между скрытым и выходным слоями). # Весовые коэффициенты связей между узлом i и узлом j следующего слоя # обозначены как w_i_j: # w11 w21 # w12 w22 и т.д. self.wih = (numpy.random.rand(self.hnodes, self.inodes) - 0.5) self.who = (numpy.random.rand(self.onodes, self.hnodes) - 0.5)
Великолепная работа! Мы реализовали то, что составляет саму сердцевину нейронной сети, - матрицы связей между ее узлами!
На следующем шаге мы улучшим этот вариант задания весовых коэффициентов.
