На этом шаге мы приведем полной код класса нейронной сети.
Мы завершили разработку класса нейронной сети. Он приведен ниже для справки, и вы можете получить его в любой момент, воспользовавшись ссылкой внизу:
# определение класса нейронной сети class neuralNetwork: # инициализировать нейронную сеть def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): # задать количество узлов во входном, скрытом и выходном слое self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes # Матрицы весовых коэффициентов связей wih (между входным и скрытым # слоями) и who (между скрытым и выходным слоями). # Весовые коэффициенты связей между узлом i и узлом j следующего слоя # обозначены как w_i_j: # w11 w21 # w12 w22 и т.д. self.wih = numpy.random.normal(0.0, pow(self.hnodes, -0.5), (self.hnodes, self.inodes)) self.who = numpy.random.normal(0.0, pow(self.onodes, -0.5), (self.onodes, self.hnodes)) # коэффициент обучения self.lr = learningrate # использование сигмоиды в качестве функции активации self.activation_function = lambda x: scipy.special.expit(x) # тренировка нейронной сети def train(self, inputs_list, targets_list): # преобразовать список входных значений в двухмерный массив inputs = numpy.array(inputs_list, ndmin=2).T targets = numpy.array(targets_list, ndmin=2).T # рассчитать входящие сигналы для скрытого слоя hidden_inputs = numpy.dot(self.wih, inputs) # рассчитать исходящие сигналы для скрытого слоя hidden_outputs = self.activation_function(hidden_inputs) # рассчитать входящие сигналы для выходного слоя final_inputs = numpy.dot(self.who, hidden_outputs) # рассчитать исходящие сигналы для выходного слоя final_outputs = self.activation_function (final_inputs) # ошибки выходного слоя = # (целевое значение - фактическое значение) output_errors = targets - final_outputs # ошибки скрытого слоя - это ошибки output_errors, # распределенные пропорционально весовым коэффициентам связей # и рекомбинированные на скрытых узлах hidden_errors = numpy.dot(self.who.T, output_errors) # обновить весовые коэффициенты для связей между # скрытым и выходным слоями self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose (hidden_outputs)) # обновить весовые коэффициенты для связей между # входным и скрытым слоями self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) # опрос нейронной сети def query(self, inputs_list): # преобразовать список входных значений # в двухмерный массив inputs = numpy.array(inputs_list, ndmin=2).T # рассчитать входящие сигналы для скрытого слоя hidden_inputs = numpy.dot(self.wih, inputs) # рассчитать исходящие сигналы для скрытого слоя hidden_outputs = self.activation_function(hidden_inputs) # рассчитать входящие сигналы для выходного слоя final_inputs = numpy.dot(self.who, hidden_outputs) # рассчитать исходящие сигналы для выходного слоя final_outputs = self.асtivation_function(final_inputs) return final_outputs
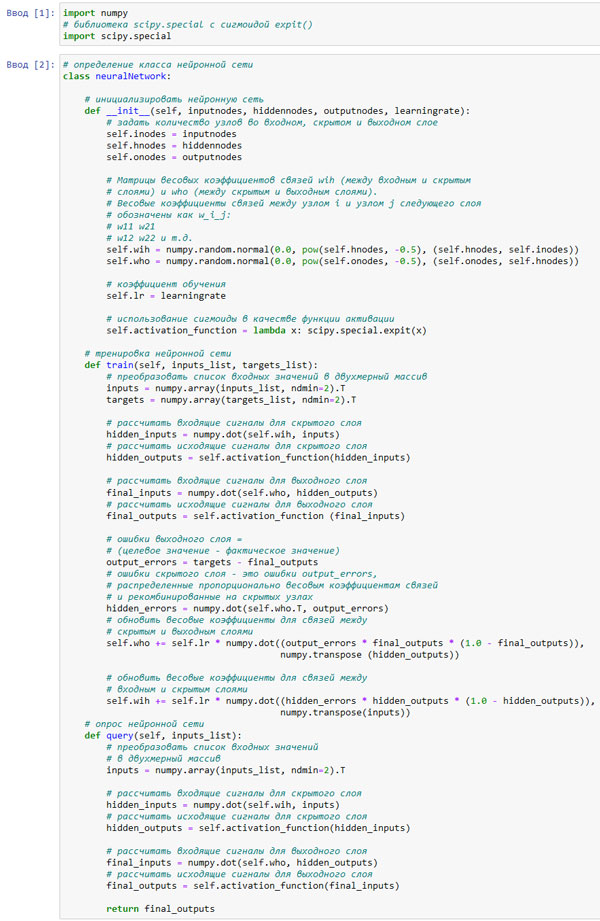
Рис.1. Блокнот с классом нейронной сети
Здесь не так много кода, особенно если принять во внимание, что он может быть использован с целью создания, тренировки и опроса трехслойной нейронной сети практически для любой задачи.
Далее мы займемся решением одной конкретной задачи: обучение нейронной сети распознаванию рукописных цифр.
На следующем шаге мы рассмотрим постановку этой задачи.
