На этом шаге мы рассмотрим простейший алгоритм обнаружения аномальных значений.

    Наблюдаемое значение считается аномальным (outlier), если отличается от среднего более чем на стандартное отклонение. Мы пройдемся по примеру анализа данных сайта в целях определения количества его активных пользователей, показателя отказов и средней длительности сеанса в секундах. (Показатель отказов (bounce rate) - это процент посетителей, которые уходят с сайта сразу же после посещения одной страницы. Высокий показатель отказов - плохой сигнал, означающий, что сайт, возможно, неинтересен или бесполезен.) Мы рассмотрим данные и выявим аномальные значения.

    Чтобы решить задачу обнаружения аномальных значений, вам сначала нужно разобраться, что такое среднее значение и стандартное отклонение, как вычислить абсолютное значение и выполнить операцию логического И.

Среднее значение и стандартное отклонение

    Во-первых, мы понемногу сформулируем определение аномального значения на основе простейших статистических понятий. Предположим, что все наблюдаемые данные нормально распределены вокруг среднего значения. Например, рассмотрим следующую последовательность значений данных:

[10.7880757  11.3598245   9.01454893 10.50119096 10.31065269  9.74358655
  9.18719987  9.48049726  9.86984107 10.26213134  7.94381676 11.52611769
  --сокращено--
 11.3020035  10.72546419]

    Если построить гистограмму этой последовательности, то получится вот что (рисунок 1).

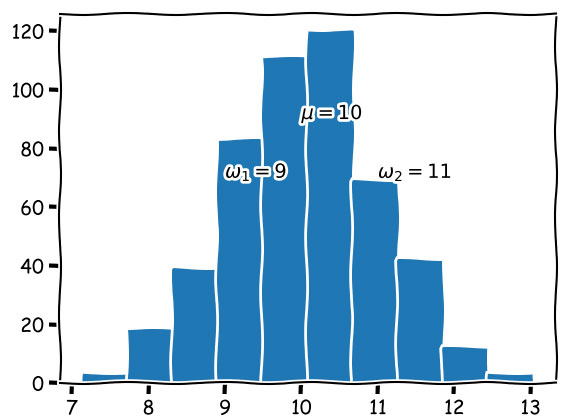
Рис.1. Гистограмма последовательности значений данных

    Эта последовательность напоминает нормальное распределение с математическим ожиданием 10 и стандартным отклонением 1. Математическое ожидание, обозначаемое символом μ, представляет собой среднее значение по всем значениям последовательности. Стандартное отклонение, обозначаемое символом σ, представляет собой меру отклонения набора данных от среднего значения. По определению, в случае истинно нормального распределения данных 68,2% всех точек данных попадает в интервал стандартного отклонения [ω₁ = μ - σ, ω₂ = μ + σ]. Из этого следует определение аномальных значений: любое значение, не попадающее в упомянутый интервал, - аномальное.

    В этом примере мы сгенерировали данные из нормального распределения с μ = 10 и σ = 1, в результате чего получается интервал ω₁ = μ - 1 = 9 и ω₂ = μ + 1 = 11. В дальнейшем мы просто предполагаем, что любое наблюдаемое значение, выходящее за пределы интервала, определяемого стандартным отклонением от математического ожидания, - аномальное. Применительно к нашим данным это означает, что любое значение, выходящее за рамки интервала [9, 11] - аномальное.

    Простой код, с помощью которого сгенерирован данный график, приведен в примере 3.25. Попробуйте найти в нем строки с описанием математического ожидания и стандартного отклонения.

import numpy as np
import matplotlib.pyplot as plt

sequence = np.random.normal(10.0, 1.0, 500)
print(sequence)
plt.xkcd()
plt.hist(sequence)
plt.annotate(r"$\omega_1=9$", (9, 70))
plt.annotate(r"$\omega_2=11$", (11, 70))
plt.annotate(r"$\mu=10$", (10, 90))
plt.savefig("plot.jpg")
plt.show()

    Код демонстрирует, как построить гистограмму с помощью библиотеки Matplotlib для Python. Однако для нас здесь это не главное; мы лишь хотели подчеркнуть, как можно сгенерировать вышеупомянутую последовательность значений данных.

    Достаточно просто импортировать библиотеку NumPy и воспользоваться модулем np.random, предоставляющим функцию normal(математическое_ожидание, отклонение, форма), создающую новый массив NumPy, значения которого выбраны из нормального распределения с заданными математическим ожиданием и стандартным отклонением. Именно при ее вызове мы задаем математическое_ожидание=10.0 и отклонение=1.0 для создания данных в последовательности. В данном случае параметр форма=500 указывает, что мы хотим получить одномерный массив данных, включающий 500 точек данных. Оставшийся код импортирует специальный стиль отрисовки графиков plt.xkcd(), строит с помощью функции plt.hits(последовательность) гистограмму на основе сгенерированной последовательности с нужными метками и выводит полученный график.

Название графика xkcd взято с популярной страницы веб-комиксов xkcd (https://xkcd.com/).

    Прежде чем заняться исследованием нашего однострочника, вкратце рассмотрим два оставшихся навыка, которые нам понадобятся, чтобы довести до конца решение нашей задачи.

Поиск абсолютного значения

    Во-вторых, нам придется преобразовывать отрицательные значения в положительные, чтобы проверить, отклоняется ли потенциальное аномальное значение от среднего более чем на стандартное отклонение. Нам важен только модуль отклонения, а не его знак. Это и называется абсолютным значением. Функция библиотеки NumPy в примере 3.26 создает новый массив NumPy, содержащий модули значений исходного массива.

import numpy as np

a = np.array([1, -1, 2, -2])
print(a)
# [1 -1 2 -2]

print(np.abs(a))
# [1 1 2 2]

    Функция np.abs() преобразует отрицательные значения массива NumPy в соответствующие им положительные.

Операция логического И

    В-третьих, следующая функция NumPy производит поэлементную операцию логического И, объединяя два булевых массива а и b и возвращая массив, значения в котором представляют собой комбинацию отдельных булевых значений из тех массивов с помощью операции логического И (пример 3.27).

import numpy as np

a = np.array([True, True, True, False])
b = np.array([False, True, True, False])
print(np.logical_and(a, b))
# [False True True False]

    Мы сочетаем элемент массива a с индексом i и элемент массива b с таким же индексом, обратившись к операции np.logical_and(a, b). Результат представляет собой массив булевых значений, равных True, если оба операнда a[i] и b[i] равны True, и False в противном случае. Это позволяет схлопывать несколько булевых массивов в один с помощью стандартных логических операций. Один из удобных сценариев применения этого - объединение массивов булевых фильтров, подобно тому, как это было сделано в предыдущем однострочнике.

    Обратите внимание: можно умножить и два булева массива a и b, что также эквивалентно логической операции np.logical_and(a, b). Дело в том, что Python представляет значение True как целочисленное значение 1 (или даже любое отличное от 0 целочисленное значение), а значение False - как целочисленное значение 0. Если умножить что-либо на 0, то получится 0, то есть False. Это значит, что True (целочисленное значение ≠ 0) получится только тогда, когда все операнды равны True.

    С этими знаниями вы теперь полностью готовы понять следующий однострочный фрагмент кода.

    На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг