На этом шаге мы продемонстрируем простой и эффективный способ вычисления факториала в одной строке кода для определения максимального количества возможных перестановок в наборе данных.
Общее описание
Рассмотрим следующую задачу: английская Премьер-лига состоит из 20 футбольных команд, каждая из которых может занимать по итогам сезона одно из 20 мест в рейтинге. При фиксированном количестве в 20 команд можно вычислить, сколько существует возможных вариантов рейтинга. Обратите внимание, что вопрос не в том, сколько мест в рейтинге может занять одна команда (разумеется, ответ на этот вопрос - 20), а сколько вообще существует рейтингов всех команд. На рисунке 1 показаны всего лишь три возможных рейтинга.
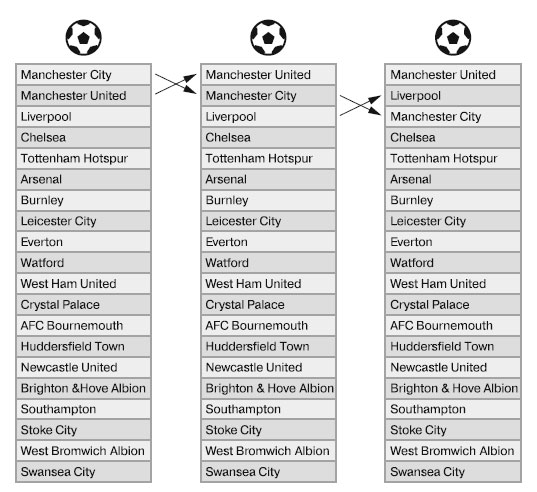
Рис.1. Три возможных рейтинга футбольных команд английской Премьер-лиги
Говоря языком теории computer science, каждый конкретный рейтинг называется перестановкой, то есть определенным порядком элементов множества. Наша задача - найти количество возможных перестановок заданного множества. Количество перестановок играет важную роль в приложениях, связанных с игрой на тотализаторе, предсказанием результатов матчей и анализом игр. Например, если начальные вероятности каждого из 100 различных рейтингов одинаковы, то вероятность каждого отдельного рейтинга равна 1/100 = 1%. Это значение может использоваться в качестве базовой (априорной) вероятности для алгоритмов предсказания результатов игр. При таких допущениях вероятность выбранного случайным образом рейтинга оказаться правильным исходом в конце сезона равна 1%.
Вычислить количество перестановок заданного множества из n элементов можно с помощью функции факториала n!. Из следующих нескольких абзацев вы узнаете почему. Определение факториала выглядит следующим образом:
n! = n × (n - 1) × (n - 2) × . . . × 1.
1! = 1 3! = 3 × 2 × 1 = 6 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3 628 800 20! = 20 × 19 × 18 × . . . × 3 × 2 × 1 = 2 432 902 008 176 640 000.
Посмотрим, как работает эта функция. Пусть дано множество из 10 элементов S = {s0, s1, s2, ... , s9} и 10 корзин B = {b0, b1, b2, ... , b9}. Мы хотим поместить в каждую корзину ровно один элемент из множества S. В нашем футбольном примере 20 команд играют роль элементов, а позиции рейтинга - роль корзин. Каждая конкретная перестановка множества S получается просто путем помещения всех элементов во все корзины. Количество различных способов распределения элементов по корзинам и будет общим количеством перестановок элементов множества S.
Количество перестановок множества из десяти элементов (которые необходимо разместить по десяти корзинам) можно определить с помощью следующего алгоритма.
- Берем первый элемент из множества S. Пустых корзин - десять, так что у нас десять вариантов того, куда поместить данный элемент. Помещаем этот один элемент в какую-то корзину.
- Одна корзина уже занята. Берем из множества S еще один элемент. Осталось девять пустых корзин, а значит, девять вариантов.
- Наконец, берем из множества S десятый (последний) элемент. Девять корзин уже занято. Осталась только одна пустая корзина, а значит, только один вариант.
В целом получаем 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 10! вариантов. Каждое из потенциальных размещений элементов по корзинам соответствует одной перестановке элементов множества. Следовательно, количество перестановок элементов множества из n элементов равно n!.
Рекурсивно функцию факториала можно определить следующим образом:
n! = n × (n - 1)!
1! = 0! = 1.
Интуитивно эти значения понятны, поскольку у множества из одного элемента существует только одна возможная перестановка, как и у множества из нуля элементов
(существует только один способ распределения нуля элементов по нулю корзин).
Код
Однострочник из примера 6.3 вычисляет количество n! перестановок множества из n элементов.
## Данные n = 5 ## Однострочник factorial = lambda n: n * factorial(n-1) if n > 1 else 1 ## Результат print(factorial(n))
Попробуйте догадаться, какой результат вернет этот код.
Принцип работы
В этом коде используется рекурсивное определение факториала. Вкратце формализуем наше интуитивное представление о рекурсии. Стивен Хокинг придумал лаконичный способ пояснить, что такое рекурсия: "Чтобы понять, что такое рекурсия, нужно сначала понять, что такое рекурсия".
Словарь Merriam-Webster дает определение рекурсии как "методики программирования компьютеров, при котором функция вызывает саму себя один или несколько раз до тех пор, пока не выполнится определенное условие, причем остальные вызовы при каждом из этих повторов обрабатываются, начиная с последнего вызова и заканчивая первым". Краеугольный камень этого определения - рекурсивная функция, то есть просто функция, вызывающая сама себя. Но если функция вызывает сама себя, то ее выполнение никогда не закончится. Поэтому задается определенное граничное условие. По его достижении последний вызов функции завершается и возвращает результат в предпоследний вызов. Предпоследний вызов, в свою очередь, возвращает результат в предпредпоследний вызов. Возникает цепная реакция распространения результатов на верхние уровни рекурсии до тех пор, пока первый вызов не вернет вызывающей стороне окончательный результат. Возможно, эту идею непросто изложить в нескольких строках, но потерпите немного: мы обсудим ее далее на примере нашего однострочника.
В общем случае создание рекурсивной функции f() включает четыре этапа.
- Разбиение исходной задачи на меньшие подзадачи.
- Использование этих меньших подзадач в качестве входных данных для функции f() (которая затем разобьет их на еще меньшие шаги и т. д.).
- Описание граничного случая (base case) - минимального варианта входных данных, вычисление которого возможно без дальнейших вызовов функции f().
- Указание способа объединения полученных меньших результатов в общий результат.
Мы создали лямбда-функцию с одним аргументом n и присвоили ее переменной factorial. Далее мы вызвали поименованную функцию factorial(n - 1) для вычисления результата вызова функции factorial(n). Значение n может представлять собой количество футбольных команд в премьер-лиге (n=20) или любое другое значение, например, как в примере 6.3 (см. выше).
Попросту говоря, мы формируем более сложное решение задачи factorial(n), умножая более простое решение factorial(n - l) на входной аргумент n. По достижении граничного случая n <= 1 мы просто возвращаем "жестко зашитое" в код решение factorial(l) = factorial(0) = 1.
Данный алгоритм демонстрирует: если сначала тщательно обдумать задачу, то часто можно найти простой, лаконичный и эффективный способ ее решения. Выбор простейшего решения - один из важнейших элементов создания собственных алгоритмов. Начинающие часто замечают, что пишут громоздкий и переусложненный код.
В данном случае рекурсивное (однострочное) определение факториала короче итеративного (однострочного) определения без рекурсии. В качестве упражнения попробуйте переписать этот однострочник без рекурсии и без внешних библиотек - это отнюдь не тривиально и явно потребует намного более длинного кода!
На следующем шаге мы рассмотрим вычисление расстояния Левенштейна.
