На этом шаге мы закончим изучение этого вопроса.
Код
С помощью этого однострочника мы напишем алгоритм для поиска всех простых чисел, не превышающих максимального целого числа m, более эффективный, чем наша наивная реализация. Однострочник в примере 6.9 основывается на древнем алгоритме под названием "решето Эратосфена", о котором мы расскажем на этом шаге.
Пример 6.9. Однострочное решение, реализующее решето Эратосфена
## Зависимости from functools import reduce ## Данные n = 100 ## Однострочник primes = reduce(lambda r, x: r - set(range(x ** 2, n, x)) if x in r else r, range(2, int(n ** 0.5) + 1), set(range(2, n))) ## Результат print(primes) # {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, # 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}
Вероятно, вам понадобятся еще некоторые предварительные знания, чтобы понять происходящее.
Принцип работы
Откровенно говоря, у нас были сомнения, включать ли этот однострочник из-за его запутанности, сложности и неудобочитаемости. Тем не менее именно такой
код вы встретите на практике, и мы хотели бы, чтобы вы смогли понять каждую его строку, даже если это займет немало времени.
Алгоритм решета Эратосфена
По существу, данный алгоритм создает огромный массив чисел, от 2 до m, заданного максимального целого числа. Все числа в массиве - кандидаты на роль простых чисел, то есть алгоритм считает их потенциально (но не обязательно) простыми. В ходе алгоритма кандидаты, которые не могут быть простыми, отсеиваются. И лишь оставшиеся после этого процесса фильтрации числа окончательно считаются простыми.
Для этого алгоритм вычисляет и помечает в массиве те числа, которые не являются простыми. В конце его выполнения все непомеченные числа - заведомо простые.
Данный алгоритм повторяет следующие шаги.
- Начинает с первого числа 2 и увеличивает его на единицу на каждом шаге процесса до тех пор, пока не будет найдено простое число х. Мы знаем,
что x простое, если оно осталось непомеченным, ведь в этом случае ни одно меньшее x число не является его делителем, а это и есть определение простого числа.
- Помечаем все числа, кратные x, поскольку они также не являются простыми: делителем для них является число x.
- Простая оптимизация: начинаем помечать кратные числа, начиная с числа x × x, а не 2x, поскольку все числа между 2x и x × x уже помечены.
Существует простое математическое доказательство этого факта, которое мы опишем далее. А пока просто поверьте, что можно начинать помечать с x × x.
Этот алгоритм показан пошагово на рисунках с 1 по 6.
Изначально все числа от 2 до m = 100 не помечены (незакрашенные ячейки). Первое непомеченное число - 2 - простое.
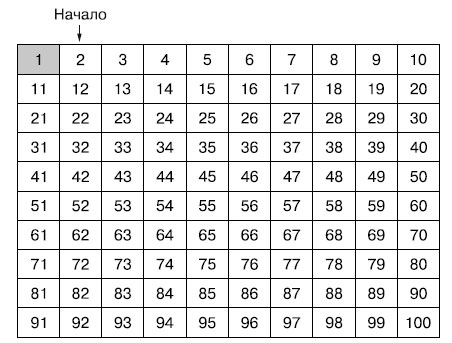
Рис.1. Начальное состояние решета Эратосфена
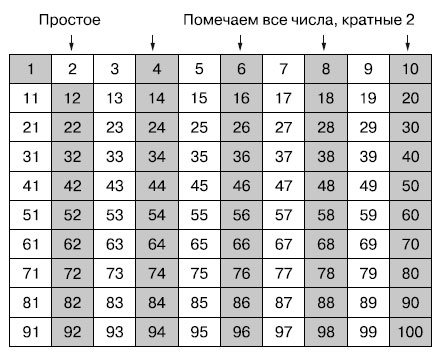
Рис.2. Помечаем все числа, кратные 2, как не простые. Игнорируем в оставшейся части алгоритма все помеченные числа
Переходим к следующему непомеченному числу, 3. Поскольку оно еще не помечено, значит, простое: мы пометили все числа, кратные числам меньше текущего числа 3, так что никакое меньшее число не является его делителем. И, по определению, число 3 - простое. Помечаем все числа, кратные 3, поскольку они - не простые, начиная с числа 3 × 3, так как все кратные 3 числа между 3 и 3 × 3 = 9 уже помечены.
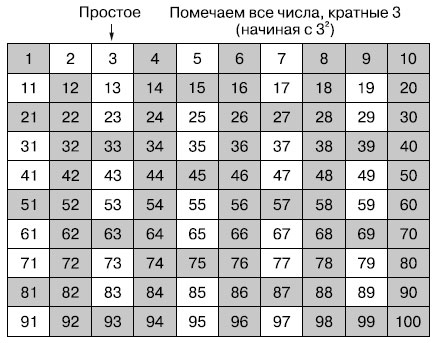
Рис.3. Помечаем все числа, кратные 3, как не простые
Переходим к следующему непомеченному числу, 5 (которое тоже простое). Помечаем все числа, кратные 5. Начинаем с числа 5 × 5, поскольку все кратные 5 числа между 5 и 5 × 5 = 25 уже помечены.
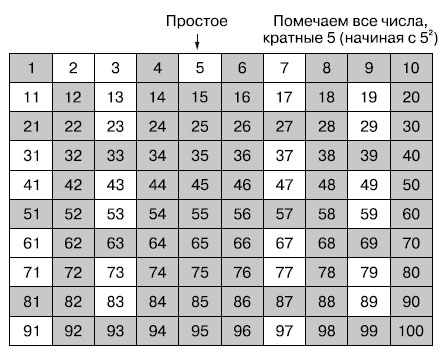
Рис.4. Помечаем все числа, кратные 5, как не простые
Переходим к следующему непомеченному числу, 7 (которое тоже простое). Помечаем все числа, кратные 7. Начинаем с числа 7 × 7, поскольку все кратные 7 числа между 7 и 7 × 7 = 49 уже помечены.
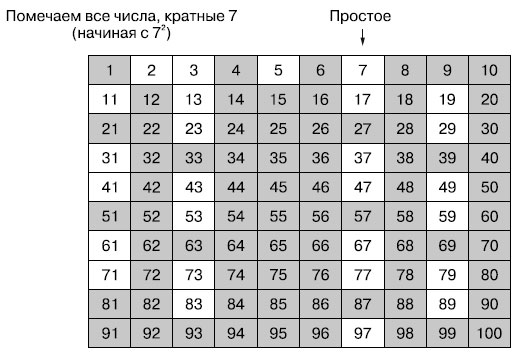
Рис.5. Помечаем все числа, кратные 7, как не простые
Переходим к следующему непомеченному числу, 11 (которое тоже простое). Помечаем все числа, кратные 11. Мы должны начать с числа 11 × 11 = 121, но понимаем, что оно превышает наш максимум m = 100. Так что алгоритм завершается. Все оставшиеся непомеченными числа не делятся ни на какое число, а значит, являются простыми.
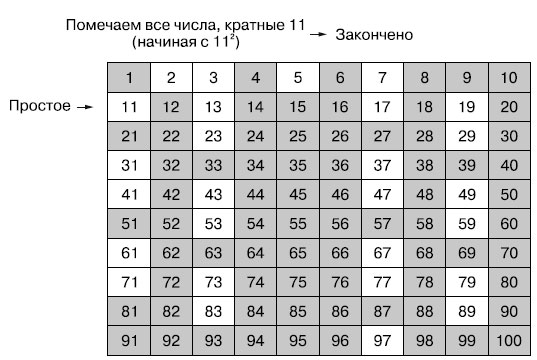
Рис.6. Помечаем все числа, кратные 11, как не простые
Решето Эратосфена намного эффективнее, чем "наивный" алгоритм, поскольку последний проверяет все числа независимо друг от друга, без учета всех предыдущих вычислений. Решето же Эратосфена, напротив, повторно использует результаты предыдущих шагов вычислений - частый прием во многих сферах оптимизации алгоритмов. Каждый раз, вычеркивая число, кратное простому, мы, по существу, избавляем себя от утомительной работы по проверке того, является ли это число простым: мы заранее знаем, что оно им не является.
Наверное, вы недоумеваете, почему мы начинаем помечать числа с квадрата простого, а не самого простого. Например, в алгоритме на рисунке 5 мы только что
обнаружили простое число 7 и начали помечать с числа 7 × 7 = 49. Дело в том, что все остальные кратные числа (7 × 2, 7 × 3, 7 × 4, 7 × 5, 7 × 6)
мы уже пометили на предыдущих итерациях, когда помечали числа, кратные всем числам, меньшим нашего текущего простого числа 7: 2, 3, 4, 5, 6.
Пояснения к однострочнику
Досконально понимая алгоритм, мы можем наконец приступить к изучению нашего однострочного решения:
## Однострочник primes = reduce(lambda r, x: r - set(range(x ** 2, n, x)) if x in r else r, range(2, int(n ** 0.5) + 1), set(range(2, n)))
В этом однострочнике для удаления по одному всех помеченных чисел из начального множества чисел от 2 до n (в однострочнике: set(range(2, n))) используется функция reduce().
Это множество служит начальным значением множества непомеченных значений r, поскольку изначально все значения не помечены. Далее однострочник проходит по всем числам x от 2 до квадратного корня из n (в однострочнике: range(2, int(n ** 0.5) + 1)) и удаляет из множества r все числа, кратные x (начиная с x ** 2), но только если число x - простое, то есть не удалено на текущий момент из множества r.
Потратьте 5-15 минут, чтобы прочитать это объяснение снова, и внимательно изучите все части данного однострочника. Обещаем, что вы потратите это время не напрасно и в результате существенно улучшите свои навыки понимания кода на языке Python.
На следующем шаге мы рассмотрим вычисление последовательности Фибоначчи с помощью функции reduce().
