На этом шаге мы рассмотрим простой алгоритм, который обязан знать любой специалист по computer science: алгоритме бинарного поиска. У бинарного поиска есть множество важных приложений во многих реализациях простых структур данных: множеств, деревьев, ассоциативных массивов, хешированных множеств, хешированных таблиц, хеш-карт и массивов. Эти структуры данных используются в любой нетривиальной программе.

    Если коротко, алгоритм бинарного поиска (binary search algorithm) производит в отсортированной последовательности l поиск конкретного значения x путем многократного сокращения размера этой последовательности вдвое, до тех пор, пока не останется только одно значение. Либо это будет искомое значение, либо его вообще не было в последовательности. Далее мы рассмотрим эту общую идею подробнее.

    Например, представьте, что нужно найти в отсортированной последовательности значение 56. При "наивном" алгоритме мы бы начали с первого элемента списка, проверили, не равен ли он 56, и перешли к следующему, и так до тех пор, пока не проверили бы все элементы или нашли искомое значение. В наихудшем случае алгоритм проверяет все элементы списка. Отсортированный список из 10 000 значений требует примерно 10 000 операций для проверки всех элементов списка на равенство искомому значению. На языке теории алгоритмов можно сказать, что сложность вычисления линейна относительно количества элементов списка. Алгоритм не использует всю доступную информацию, чтобы добиться максимальной эффективности.

    Первая часть полезной информации - то, что список отсортирован! С помощью этого факта можно создать алгоритм, которому, чтобы абсолютно точно выяснить, присутствует ли в списке искомый элемент, достаточно проверить лишь несколько элементов списка. Алгоритм бинарного поиска обходит лишь log₂(n) элементов (логарифм по основанию 2). Для поиска в том же списке из 10 000 элементов достаточно всего лишь log₂(10 000) < 14 операций.

    При бинарном поиске предполагается, что список отсортирован в порядке возрастания. Алгоритм проверяет сначала элемент в середине списка. Если это срединное значение больше искомого, значит, все значения от середины и до последнего элемента списка больше требуемого. Искомое значение не входит в эту половину списка, так что одной операции достаточно, чтобы сразу отбросить половину элементов.

    Аналогично, если искомое значение больше срединного, то можно отбросить первую половину элементов списка. А затем эта процедура сокращения вдвое фактического размера списка проверяемых элементов повторяется на каждом шаге алгоритма. На рисунке 1 приведен наглядный пример.

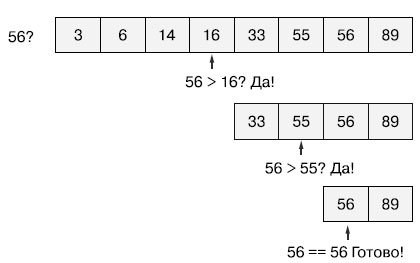
Рис.1. Пример работы алгоритма бинарного поиска

    Если подсписок содержит четное количество элементов, то явного срединного элемента не существует. В этом случае мы округляем индекс срединного элемента.

    Нам нужно найти значение 56 в отсортированном списке из восьми целочисленных значений, просмотрев при этом как можно меньше элементов. Алгоритм бинарного поиска проверяет расположенный посередине (с учетом округления) элемент x и отбрасывает половину списка, в которой 56 заведомо не может быть. У этой проверки могут быть три исхода:

• элемент x больше 56. Алгоритм игнорирует правую часть списка;
• элемент x меньше значения 56. Алгоритм игнорирует левую часть списка;
• элемент x равен 56, как на последней строке рисунка 1. Поздравляем - мы нашли искомое значение!

    В пример 6.12 показана реализация алгоритма бинарного поиска.

def binary_search(lst, value):
    lo, hi = 0, len(lst) - 1
    while lo <= hi:
        mid = (lo + hi) // 2
        if lst[mid] < value:
            lo = mid + 1
        elif value < lst[mid]:
            hi = mid - 1
        else:
            return mid
    return -1


l = [3, 6, 14, 16, 33, 55, 56, 89]
x = 56
print(binary_search(l, x))
# 6 (индекс найденного элемента)

    Этот алгоритм получает в качестве аргумента список и значение для поиска, после чего последовательно делит пополам область поиска с помощью двух переменных lo и hi, задающих интервал элементов списка, в котором может находиться искомое значение: lo задает начальный индекс данного интервала, а hi - конечный. Мы проверяем, какой из вышеупомянутых случаев имеет место для срединного элемента, и подгоняем интервал поиска соответствующим образом, модифицируя значения lo и hi.

    И хотя это вполне нормальная, удобочитаемая и эффективная реализация алгоритма бинарного поиска, она занимает отнюдь не одну строку!

    На следующем шаге мы закончим изучение данного вопроса.

Предыдущий шаг Содержание Следующий шаг