На этом шаге мы создадим однострочник для популярного алгоритма быстрой сортировки (Quicksort) - алгоритма сортировки, который, как ясно из его названия, быстро сортирует данные.
Быстрая сортировка - частый вопрос на многих собеседованиях (его задают в Google, Facebook и Amazon), а также быстрый, лаконичный и удобочитаемый алгоритм сортировки. Благодаря изяществу быстрой сортировки о ней рассказывается в большинстве курсов для начинающих.
Быстрая сортировка сортирует список путем рекурсивного разбиения большой задачи на меньшие и объединения решений этих меньших задач так, чтобы получить решение большей.
Для решения каждой из меньших задач используется рекурсивно та же стратегия: меньшие задачи разбиваются на еще меньшие подзадачи, решаемые по отдельности и объединяемые, так что быстрая сортировка относится к алгоритмам, работающим по принципу разделяй и властвуй.
При быстрой сортировке выбирается опорный элемент (pivot element), а затем все элементы, которые больше него, помещаются справа от него, а все элементы, которые меньше или равны ему, - слева. Таким образом, большая задача сортировки списка разбивается на две меньшие подзадачи сортировки двух меньших списков. А затем эта процедура повторяется рекурсивно до тех пор, пока не получится список из нуля элементов, попытка сортировки которого приводит к завершению рекурсии.
На рисунке 1 показан алгоритм быстрой сортировки в действии.
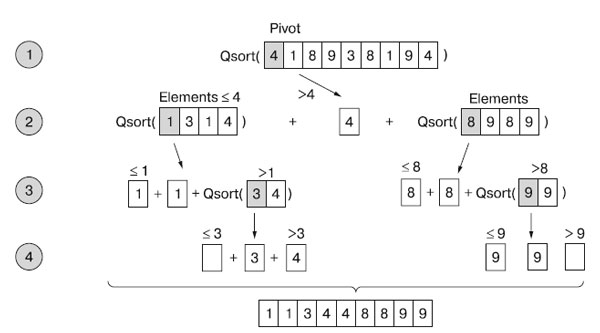
Рис.1. Пример работы алгоритма быстрой сортировки
На рисунке 1 показано применение алгоритма быстрой сортировки к неотсортированному списку целых чисел [4, 1, 8, 9, 3, 8, 1, 9, 4]. Сначала он выбирает 4 в качестве опорного элемента, разбивает список на неотсортированный подсписок [1, 3, 1, 4], все элементы которого меньше или равны опорному, и неотсортированный подсписок [8, 9, 8, 9], все элементы которого больше опорного.
Далее алгоритм быстрой сортировки вызывается рекурсивно для сортировки двух неотсортированных подсписков. Как только размер подсписков доходит до не более чем одного элемента, считается, что они отсортированы по определению, и рекурсия завершается.
На каждом шаге рекурсии производится конкатенация трех подсписков (левого, опорного и правого) перед передачей итогового списка на более высокий уровень рекурсии.
На следующем шаге мы закончим изучение этого вопроса.
