На этом шаге мы рассмотрим особенности такого вычисления.

Согласно представленной в таблице 1 на 20 шаге методике первый шаг состоит из определения размера задачи, который зависит от входных параметров. В этой задаче для определения числа операций в алгоритме вычисления степени важен лишь показатель степени. Ясно, что время выполнения растёт с ростом n, поскольку результат требует большего количества умножений. Таким образом, размер задачи - это показатель степени n. Начальное условие соответствует тривиальным экземплярам задачи минимального размера. Так как n - неотрицательное целое число, наименьший экземпляр класса - это b₀, равный 1.

На этапе декомпозиции нужно рассмотреть наименьшую и простейшую из подзадач, подобных исходной, которая получается путём уменьшения размера исходной задачи. На этом шаге мы будем уменьшать её размер на 1, что приведёт к следующей схеме:

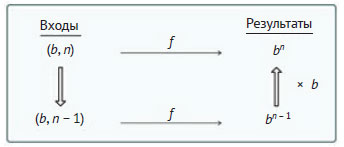
где f(b, n) = bⁿ - функция от двух параметров b и n. Очевидно, если нам известно решение f(b, n - 1) = b^n-1, то в рекурсивном условии остаётся сделать лишь одно - умножить её на b, чтобы получить bⁿ. Функцию вместе с её начальным условием можно реализовать, как показано в примере 4.1.

Пример 4.1. Степенная функция для неотрицательных степеней с линейным временем выполнения

1
2
3
4
5

def power_linear(b, n):
    if n == 0:
        return 1
    else:
        return b * power_linear(b, n - 1)

Архив с файлом можно взять здесь.

Это пример линейной рекурсии, так как в рекурсивном условии есть только один вызов функции, не являющийся последней выполняемой алгоритмом операцией. Несмотря на то что вызов функции является последним элементом выражения (в строке 5), метод сначала вычисляет её и только потом умножает результат на b. Таким образом, функция не относится к хвостовой рекурсии. Также важно отметить, что функция не нуждается в начальном условии для n = 1, так как оно было бы избыточным. Наконец, вычислительная сложность этого алгоритма линейно зависит от n. В частности, время выполнения может быть определено так:

           1,        если n = 0
    T(n) =                            (4.1)
           T(n - 1), если n > 0

где T(n) = n + 1 ∈ Θ(n).

Если условием задачи допускались бы ещё и отрицательные целочисленные показатели степени, то размер задачи был бы абсолютной величиной n. В этом случае начальное условие также задаётся для n = 0, а рекурсивное условие идентично случаю n > 0. Когда n - отрицательное, декомпозиция должна уменьшать размер задачи таким образом, чтобы соответствующая подзадача стремилась к начальному условию. Таким образом, для этого рекурсивного условия необходимо увеличивать n. Схема процесса рассуждений была бы такой:

Таким образом, для получения отрицательной степени bⁿ результат подзадачи должен делиться на b. Поэтому рекурсивное условие должно быть f(b, n) = f(b, n + 1)/b, как показано в примере 4.2.

Пример 4.2. Степенная функция с линейным временем выполнения

1
2
3
4
5
6
7

def power_gtntral_linear(b, n):
    if n == 0:
        return 1
    elif n > 0:
        return b * power_gtntral_linear(b, n - 1)     
    else:
        return power_gtntral_linear(b, n + 1) / b

Архив с файлом можно взять здесь.

На следующем шаге мы рассмотрим вычисление степени за логарифмическое время.

Предыдущий шаг Содержание Следующий шаг