На этом шаге мы рассмотрим эту, более общую, задачу.

Задача из предыдущего шага - частный случай более общей задачи, которая заключается в преобразовании десятичного числа к другому основанию b, где b > 2. Её можно решить аналогично с применением схем. На рисунке 1 показаны шаги общего алгоритма решения задачи.

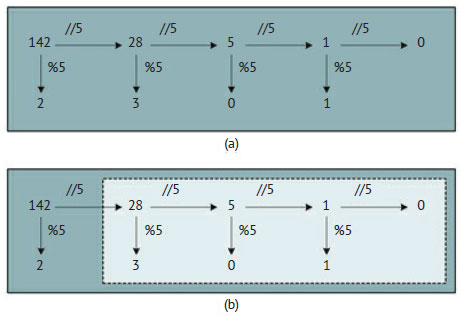
Рис.1. Приведение десятичного числа 142 к основанию 5 (1032)

В частности, он показывает, как привести десятичное число 142 к основанию 5, то есть 142₁₀ = 1032₅. Полное решение задачи показано на рисунке 1(a), идея которого состоит в последовательном выполнении целочисленного деления n на b до достижения им значения 0. На каждом шаге вычисляются также остатки от деления b, которые образуют цифры в новом представлении числа по основанию b, чьи позиции определяются степенью 10. В схеме на рисунке 1(b) подзадача (28₁₀ = 103₅) исходной задачи выделена более светлым фоном.

Для разработки рекурсивного решения нужно определить размер задачи. Для этой задачи он равен количеству делений n на b до достижения им значения 0. Количество делений - это, в сущности, количество цифр по основанию b. Начальное условие выполняется, когда n представляет собой единственную цифру по основанию b. Другими словами, если n < b, то результат равен n.

Рекурсивное условие требует идентификации подзадачи в пределах исходной, как показано на рисунке 1(b). Отметим, что подзадача подобна исходной задаче, начиная с 28 = 142//5. Таким образом, декомпозиция состоит из выполнения целочисленного деления n//b, которое уменьшает размер задачи на 1. Впоследствии нужно будет определить, как следует изменить решение подзадачи (103), чтобы получить решение исходной задачи (1032). Решение заключается в умножении результата подзадачи на 10 и добавлении к нему n%b (равного 2 в этом примере). Таким образом, функцию можно закодировать, как показано в примере 4.10.

Пример 4.10. Приведение неотрицательного целого числа n к основанию b

1
2
3
4
5

def decimal_to_base(n, b):
    if n < b:
        return n
    else:
        return 10 * decimal_to_base(n // b, b) + (n % b)

Архив с файлом можно взять здесь.

Со следующего шага мы обратимся к строкам.

Предыдущий шаг Содержание Следующий шаг