На этом шаге мы рассмотрим несколько рекурсивных решений такой сортировки.

    Этот и следующий шаг содержит несколько классических задач, которые имеют изящные рекурсивные решения.

Сортировка выбором

    Сортировки выбором - один из самых простых способов сортировки элементов списка. Для заданного списка из n чисел предложить метод его сортировки в порядке возрастания. Алгоритм начинается с поиска и размещения наименьшего элемента списка в первой позиции выходного списка. На втором шаге метод ищет минимальный элемент среди оставшихся 1...(n - 1) элементов и помещает его во вторую позицию списка вывода. Эта процедура выполняется (n - 1) раз, пока в итоге массив не отсортируется. Ясно, что в конце k-го шага наименьшие k чисел уже отсортированы, а после (n - 1) шага будет полностью отсортирован весь список.

    Теперь рассмотрим линейно-рекурсивную версию алгоритма. Во-первых, размер задачи - это длина списка (n). Начальное условие выполняется, когда список состоит из одного элемента и не нуждается в сортировке, являясь, очевидно, её результатом. Кроме того, если вход пуст, алгоритм может вернуть ещё и пустой список. Таким образом, для начального условия метод возвращает результат при n ≤ 1.

    Для вывода рекурсивного условия декомпозиция должна уменьшать размер задачи на 1, когда наименьший элемент списка исключается из него. Это можно сделать двумя способами. Во-первых, элемент можно менять местами с первым элементом списка. Это, естественно, не меняет результата (сортированного списка), но позволяет после обмена местами исключить первый элемент списка. Поэтому если входной список [7, 5, 3, 8, 4], он превращается в [3, 5, 7, 8, 4] после обмена местами 3 и 7. В этом случае входом подзадачи размера n - 1 был бы список [5, 7, 8, 4], а рекурсивная схема для этого частного примера могла бы быть такой:

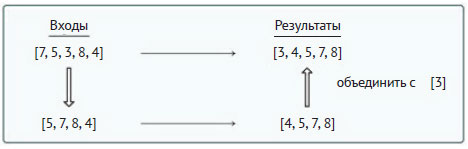
    Чтобы решить исходную задачу, рекурсивное правило должно добавить исключённый наименьший элемент ([3]) в начало выходного списка подзадачи (заметьте, что результаты - это сортированные списки). В примере 4.13 приведена реализация метода с использованием функции min() для определения наименьшего значения в списке, метода index(), возвращающего позицию элемента в списке, и операции + (конкатенация) для объединения списков. Важной деталью этого алгоритма является то, что он должен создать новую копию входного списка (в строке 5), чтобы не изменить его при вызове метода. В частности, без этой копии метод поменял бы местами первый и наименьший элементы списка.

def select_sort_rec(a):
    if len(a) <= 1:
        return a
    else:
        b = list(a)
        min_index = b.index(min(b))
        aux = b[min_index]
        b[min_index] = b[0]
        b[0] = aux

        return [aux] + select_sort_rec(b[1:])    

    Другой способ уменьшения размера задачи - исключение наименьшего элемента прямым удалением его из списка. В этом случае рекурсивная схема была бы такой:

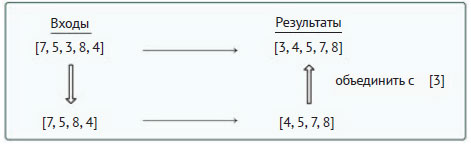
    Её единственное отличие от предыдущей схемы - порядок следования элементов во входном параметре подзадачи. Но он совершенно не влияет на рекурсивное правило, где также нужно добавлять удалённый наименьший элемент ([3]) к списку вывода подзадачи. В примере 4.14 приведена возможная реализация функции, использующая для удаления наименьшего элемента метод remove(). В строке 5 также создаётся копия входного списка, чтобы не изменить его очередным вызовом метода.

def select_sort_rec_alt(a):
    if len(a) <= 1:
        return a
    else:
        b = list(a)
        n = min(b)
        b.remove(n)

        return [n] + select_sort_rec_alt(b)    

    Наконец, оценка времени выполнения этих алгоритмов задаётся формулой (3.24), так как поиск (и удаление) наименьшего элемента списка требует порядка n операций. Таким образом, алгоритмы работают за время Θ(n²).

    На следующем шаге мы рассмотрим схему Горнера.

Предыдущий шаг Содержание Следующий шаг