На этом шаге мы рассмотрим несколько заданий и приведем их решения.

Приведем несколько примеров решения задач.

Задание 1. Пусть а - сортированный (в порядке возрастания) список различных целых чисел. Цель этой задачи - эффективный поиск элемента, значение которого совпадает с его позицией (индексом) в списке. Иными словами, нужно найти элемент i, для которого а_i = i. Например, если а = [-3, -1, 2, 5, 6, 7, 9], то результатом будет 2, так как а₂ = 2. Отметим, что первый элемент списка расположен в позиции 0. Для простоты считайте, что в а не более одного элемента, удовлетворяющего условию а_i = i. Если в списке нет такого элемента, функция должна вернуть значение -1.

Раскрыть/скрыть решение и комментарии.

Задание 2. Определите и реализуйте хвостовую рекурсивную логическую функцию, определяющую, содержит ли неотрицательное целое число n нечётную цифру.

Раскрыть/скрыть решение и комментарии.

Задание 3. Алгоритм "сортировки подсчётом" - это метод сортировки списка из n целых чисел в диапазоне [0, k], где k достаточно малое. Метод работает за время Ο(n + k), откуда следует, что он работает за время Ο(n) при k ∈ Ο(n).

Для заданного списка a метод создаёт новый список b, который содержит количество вхождений каждого целого числа в а, как показано на рисунке 1 (шаг 1).

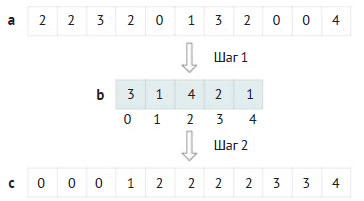
Рис.1. Шаги алгоритма сортировки подсчётом

Например, b₂ = 4, так как целое число 2 появляется в а четыре раза. Реализуйте хвостовую рекурсивную процедуру, которая получает списки а и b (изначально нулевой) и заполняет список b количествами вхождений целых чисел в a.

Кроме того, реализуйте линейно-рекурсивную функцию, которая получает список b с количествами вхождений и возвращает новый список c - отсортированную версию а, как показано на рисунке 1 (шаг 2).

Раскрыть/скрыть решение и комментарии.

Приведем сначала тексты функций.

Задание 3.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def f(a, b):
    if len(a) == 0:
        return b
    else:
        b[a[0]] += 1
        return f(a[1:], b)


def beg_f(a):
    b = [0] * (max(a) + 1)
    return f(a, b)


def f_2(b, ind):
    if len(b) == 0:
        return []
    else:
        return [ind] * b[0] + f_2(b[1:], ind + 1)    


def beg_f2(b):
    index = 0
    return f_2(b, index)

Архив с файлом можно взять здесь.

Прокомментируем приведенный текст.

Функция f(), решающая первую задачу, имеет функцию-обертку beg_f(), в которой производится создание нулевого списка b, количеством элементов, равным k + 1. На рисунке 1 максимальный элемент в списке a равен 4, поэтому количество элементов в списке b равно 5. Здесь же вызывается функция f().

Реализация этой функции достаточно проста: берем первый элемент из a и увеличиваем на 1 значение из списка b, находящееся на позиции, определяемой этим первым элементом из списка a. Снова вызываем эту же функцию, предварительно отбросив первый элемент из списка a.

Когда список a станет пустым, нужно вернуть сформированный список b.

Функция f_2(), решающая вторую задачу, имеет функцию-обертку beg_f2(), где определяется номер обрабатываемого элемента в списке b. Так как каждый раз будет отбрасываться первый элемент из списка b, нужно значение, которое будет хранить общий индекс элемента в списке b (переменная index, равная 0).

Рекурсивное соотношение простое: повторяем значение ind столько раз, сколько указано в первом элементе списка b, после чего его отбрасываем и снова вызываем функцию f_2() с увеличенным на 1 номером позиции.

Когда список b стал пустым, возвращаем пустой список.

Со следующего шага мы начнем рассматривать множественную рекурсию.

Предыдущий шаг Содержание Следующий шаг