На этом шаге мы рассмотрим более подробно решение этой задачи.

Вместо прямого подсчёта объёма всей популяции можно подсчитать число зрелых и незрелых пар для каждого месяца в отдельности. Это приводит к двум различным задачам размера n. В частности, пусть A(n) и B(n) обозначают, соответственно, количество зрелых и незрелых пар в каждом месяце n. Тогда начальными условиями будут A(1) = 0 и B(1) = 1, поскольку вначале есть только одна пара незрелых кроликов. На втором месяце появится пара кроликов, еще не способных производить потомство. Таким образом, B(2) = 0 и A(2) = 1.

Для рекурсивных условий правила роста популяции показаны на рисунке 1, где маленькие и большие кролики изображают незрелые и зрелые пары соответственно.

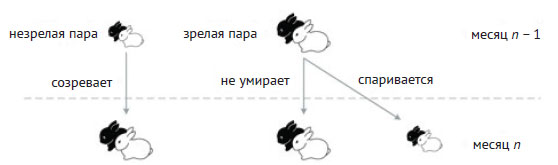
Рис.1. Правила размножения кроликов

С одной стороны, каждая пара незрелых кроликов в данном месяце созревает во взрослую пару в следующем месяце. С другой стороны, каждая зрелая пара появляется и в следующем месяце (поскольку кролики никогда не умирают), и она также спаривается, создавая новую пару потомства.

Согласно методу индукции, нам известен объём популяции зрелых и незрелых пар в месяце n - 1 (то есть A(n - 1) и B(n - 1)), откуда довольно просто вывести рекурсивные условия для A(n) и B(n). Во-первых, число незрелых пар в n-м месяце равно числу зрелых пар в прошлом месяце, поскольку зрелой паре нужен один месяц, чтобы спариться и произвести новую пару незрелых кроликов. Поэтому B(n) = A(n - 1). Что касается A(n), то все зрелые пары, жившие в месяце n - 1, будут живы и в месяце n, так как кролики не умирают. Кроме того, все незрелые пары в течение месяца n - 1 созревают и превращаются в зрелые. Таким образом, рекурсивное условие - A(n) = A(n - 1) + B(n - 1). Обе функции можно определить следующим образом:

            0,                   если n = 1,
    A(n) =                                                       (9.1)
            A(n - 1) + B(n - 1), если n > 1    ,

            1,        если n = 1,
    B(n) =                                                       (9.2)
            A(n - 1), если n > 1    .

В них не нужны явные начальные условия для n = 2, так как они - именно те самые функции, которые были введены на 14 шаге. Ясно, что A - рекурсивная функция, потому что она вызывает себя. Метод B вызывает себя косвенно - через вызов A, который, в свою очередь, вызывает B. В примере 9.3 приведён код, соответствующий этим функциям.

Пример 9.3. Взаимно-рекурсивные функции подсчёта популяции незрелых и зрелых пар кроликов спустя n месяцев

1
2
3
4
5
6
7
8
9
10
11
12

def adults(n):
    if n == 1:
        return 0
    else:
        return adults(n - 1) + babies(n - 1)    


def babies(n):
    if n == 1:
        return 1
    else:
        return adults(n - 1)

Архив с файлом можно взять здесь.

Эти функции можно выразить исключительно через самих себя, как показано в (3.38) и (3.39). Наконец, общее количество пар кроликов - это просто сумма A(n) + B(n), которая оказывается n-м числом Фибоначчи.

Нелишне напомнить, что автором этой задачи был сам Леонардо Пизанский по прозвищу Фибоначчи.

На следующем шаге мы рассмотрим родовое дерево кроликов.

Предыдущий шаг Содержание Следующий шаг