На этом шаге мы рассмотрим другое решение задачи предыдущего шага.

    В примере 10.4 приведёно иное, более простое и естественное, рекурсивное решение задачи. Вся его суть заключается в проверке наличия файла в некоторой папке (без учёта вложенных папок) и во всех вложенных в неё папках. Обратите внимание, что поиск в этих подпапках - это просто меньший экземпляр исходной задачи. Метод тоже использует цикл для проверки каждого объекта данной папки (и потому использует множественную рекурсию). Однако при обнаружении папки он вызывает сам себя для поиска заданного файла в этой папке или в любой из вложенных в неё подпапок.

    На рисунке 2 показано состояние программного стека при выполнении кода из примера 10.4 для файлов и папок на рисунке 1.

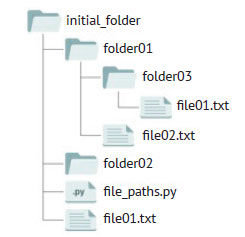
Рис.1. Пример дерева файловой системы

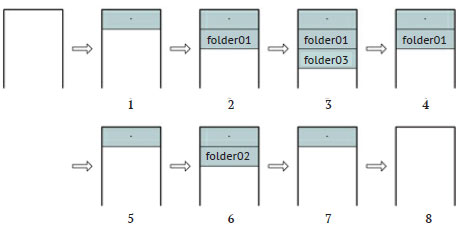
Рис.2. Выделение стековых кадров при выполнении кода из примера 10.4 для файлов и папок на рисунке 1

import os


def print_path_file_recursive(file_name, folder):
    for entry in os.scandir(folder):
        if entry.is_file() and file_name == entry.name:   
            print(entry.path)
        elif entry.is_dir():
            print_path_file_recursive(file_name, entry.path)  


print_path_file_recursive('file01.txt', '.')

    Имя в стековом кадре - это имя папки при вызове метода (имя файла - одно и то же для каждого вызова), где первый вызов метода использует начальный каталог. Как только метод обнаруживает папку F, он снова вызывает сам себя, чтобы напечатать все пути к файлу file_name в этой папке и ко всем вложенным в неё папкам. Таким образом, в алгоритме реализован тот же поиск файла в файловой системе в глубину, но при этом нет явного управления стеком. Наоборот, все действия с программным стеком скрыты от программиста.

    На этом примере мы показали, что для определённых задач рекурсивное решение может быть короче, проще (поскольку не использует стек) и легче для понимания, так как отвечает естественному ходу рассуждений при решении задачи. Кроме того, в этом примере итерационный алгоритм лишь немного эффективнее рекурсивного. Вы можете оценить время выполнения обоих алгоритмов на своих компьютерах. Наконец, благодаря удобочитаемости и простоте рекурсивные алгоритмы легче поддерживать и отлаживать. Для определённых задач эти качества могут оказаться весомее временнОй и пространственной эффективности.

    Наконец, любая рекурсивная программа может быть преобразована в итерационную (и наоборот). Суть этого преобразования - в явном использовании стека для моделирования действий с программным стеком. Например, он мог бы содержать параметры, передаваемые рекурсивным функциям. Существуют стандартные методы преобразования рекурсивного кода в итерационный, но эта тема выходит далеко за рамки данного изложения.

    Со следующего шага мы начнем знакомится с мемоизацией и динамическим программированием.

Предыдущий шаг Содержание Следующий шаг