На этом шаге мы рассмотрим рекурсивные способы его вычисления.

Цифровой корень неотрицательного целого числа n, обозначаемый здесь как d(n), вычисляется следующим образом. Сначала вычисляется сумма цифр исходного числа n, затем - сумма цифр полученной суммы и так далее до тех пор, пока очередная сумма не станет однозначным числом. Например,

  d(79868) = (7 + 9 + 8 + 6 + 8) = 38 → d(38) = (3 + 8) = 11 → d(11) = (1 + 1) = 2 → d(2) = 2.

Размер задачи зависит от количества цифр n, а к начальному условию задачи мы, очевидно, приходим, когда n состоит из одной цифры.

Для рекурсивного условия можно предложить два варианта. Во-первых, по условию задачи n заменяется суммой своих цифр, что приводит к следующему определению цифрового корня:

           n,       если n < 10
    d(n) = 
           d(s(n)), если n ≥ 10

где s(n) - функция суммирования цифр неотрицательного целого числа (см. пример 2.2). Заметьте, что это - хвостовая рекурсивная функция.

Второй вариант подразумевает уменьшение размера задачи путём отбрасывания одной из цифр n. Рассмотрим следующую конкретную рекурсивную схему:

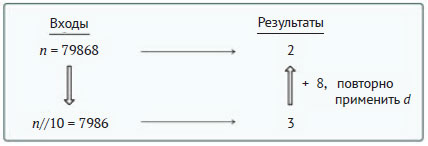
Рекурсивное условие требует добавления последней цифры n к результату подзадачи и повторного применения того же метода. Таким образом, функцию можно определить исключительно через саму себя:

           n,                      если n < 10
    d(n) = 
           d(d(n // 10) + n % 10), если n ≥ 10

что является примером вложенной рекурсии. Такую функцию легко закодировать (см. пример 11.8).

Пример 11.8. Метод с вложенной рекурсией для вычисления цифрового корня неотрицательного целого числа

1
2
3
4
5

def digital_root(n):
    if n < 10:
        return n
    else:
        return digital_root(digital_root(n // 10) + n % 10)

Архив с файлом можно взять здесь.

Наконец, функция d обладает многими свойствами, которые включают в себя вложенную рекурсию. Например,

  d(n + m) = d(d(n) + d(m)) или d(n ⋅ m) = d(d(n) ⋅ d(m)).

На следующем шаге мы перейдем к хвостовой и вложенной рекурсии через обобщённую функцию.

Предыдущий шаг Содержание Следующий шаг