На этом шаге мы рассмотрим реализацию этого алгоритма.

    Поскольку решением задачи является подмножество множества из n предметов, можно разработать алгоритм, дерево рекурсии которого подобно двоичным деревьям рекурсии алгоритмов генерации подмножеств или сумм подмножеств. На рисунке 1 приводится дерево рекурсии для весов w = [3, 6, 9, 5], стоимостей v = [7, 2, 10, 4] и грузоподъёмности рюкзака C = 15, которые будут входными параметрами рекурсивного метода.

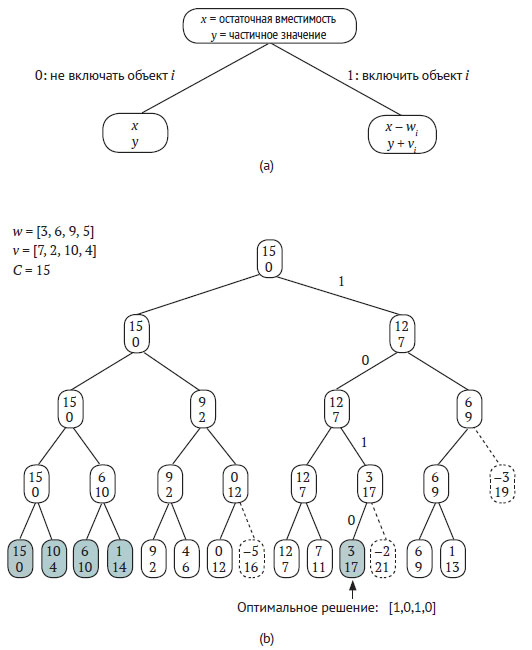
Рис.1. Дерево рекурсии алгоритма перебора с возвратами для задачи о рюкзаке 0-1

    Узлы дерева - это вызовы метода с конкретным частичным решением в качестве параметра, а числа в узлах - это весовой остаток рюкзака и суммарная стоимость уже помещённых в него предметов (см. рисунок1(а)). Для каждого индекса i в частичном решении алгоритм либо не помещает (левый потомок узла), либо помещает (правый потомок узла) предмет в рюкзак. Если предмет не помещён в рюкзак, то обе величины в дочернем узле не меняются. Если же предмет помещён в рюкзак, то весовой остаток рюкзака уменьшается на w_i, а его суммарная стоимость увеличивается на v_i. Поскольку алгоритм решает задачу оптимизации, он должен хранить найденное на предыдущих шагах лучшее решение, чтобы обновлять его при обнаружении ещё лучшего решения.

    Полное дерево рекурсии приведено на рисунке 1(b), где затемнённые узлы обозначают вызовы метода, которые обновляют это лучшее решение. Если оптимальной суммарной стоимости рюкзака сразу присвоить отрицательное начальное значение, то метод обновит оптимальное решение уже в первом листе дерева. В этом случае частичное решение будет пустым множеством, а суммарная стоимость - нулевой. Продолжив обход дерева, метод обновит лучшее решение после добавления в рюкзак самого последнего предмета (w₃ = 5 и v₃ = 4) так, что весовой остаток рюкзака в листовом узле будет равен 10, а общая стоимость частичного решения - 4. В процессе решения задачи лучшее решение будет обновлено ещё трижды для суммарных стоимостей 10, 14 и 17. Последнее обновление, естественно, даст оптимальное решение задачи. В данном случае это подмножество, состоящее из первого и третьего предметов, а максимальная сумма стоимостей - 17. В заключение важно отметить, что метод сокращает двоичное дерево рекурсии в тех случаях, когда весовой остаток рюкзака для частичного решения (и узла) - отрицательный.

    В примере 12.12 приведена возможная реализация алгоритма перебора с возвратами.

def knapsack_0_1(i, w_left, current_v, sol,
                 opt_sol, opt_v, w, v, C):
    # Проверить базовый вариант
    if i == len(sol):
        # Проверить, найдено ли лучшее решение.
        if current_v > opt_v:
            # Обновить оптимальное значение и решение
            opt_v = current_v
            for k in range(0, len(sol)):
                opt_sol[k] = sol[k]

    else:
        # Генерация кандидатов
        for k in range(0, 2):

            # Проверить, можно ли обрезать дерево рекурсии
            if k * w[i] <= w_left:
                # Развернуть частичное решение
                sol[i] = k

                # Обновите оставшийся набор и частичное значение  
                new_w_left = w_left - k * w[i]
                new_current_v = current_v + k * v[i]

                # Попробовать развернуть частичное решение
                opt_v = knapsack_0_1(i + 1, new_w_left,
                                     new_current_v, sol,
                                     opt_sol, opt_v, w, v, C)

    # Возврат оптимального решения, найденного на данный момент
    return opt_v


def knapsack_0_1_wrapper(w, v, C):
    sol = [0] * (len(w))
    opt_sol = [0] * (len(w))
    total_v = knapsack_0_1(0, C, 0, sol, opt_sol, -1, w, v, C)
    print_knapsack_solution(opt_sol, w, v, C, total_v)

    Во-первых, подобно другим методам, его входные параметры включают частичное решение sol и индекс i предмета, который можно поместить в рюкзак.

    Метод получает ещё списки весов w и стоимостей v, а также грузоподъёмность рюкзака C. По этим параметрам можно на любом шаге вычислить и весовой остаток, и суммарную стоимость предметов в рюкзаке. Но гораздо эффективнее ввести для хранения этих величин два дополнительных параметра w_left - для весового остатка и current_v - для суммарной стоимости предметов. Их преимущество в том, что они легко и быстро обновляются, не требуя дополнительных вычислений.

    Кроме того, метод во время выполнения сохраняет лучшее из найденных решений. Оно хранится в параметре opt_sol, который является копией того частичного решения, которое получено по достижении листа дерева рекурсии. Наконец, opt_v содержит оптимальную суммарную стоимость opt_sol. Этот параметр тоже избыточен в том смысле, что его значение можно вычислить по opt_sol, но ради дополнительной эффективности его значение лучше передавать как параметр.

    Как обычно, рекурсивная функция начинается с проверки начального условия. Если метод достиг полного решения (строка 4), он в строке 6 сравнивает стоимости текущего sol и лучшего opt_sol решений, полученных на предыдущих шагах. Если стоимость sol превышает стоимость opt_sol, метод обновляет opt_v и opt_sol. Позже, в строке 31, метод вернёт в качестве своего результата opt_v. Значения списка opt_ sol тоже будут доступны по завершении метода, поскольку этот список передаётся в метод по ссылке и, следовательно, меняется в процессе поиска решения.

    В рекурсивном условии метод в строке 13 генерирует кандидатов (со значениями 0 или 1) для включения в двоичный список частичного решения. Затем, с целью сократить дерево рекурсии, он проверяет условие k * w[i] <= w_left. Если k = 0, предмет не добавляется в рюкзак, и условие всегда истинно, так как w_left - неотрицательная величина. Если же k = 1, алгоритм добавляет предмет в рюкзак, если это возможно, то есть если w_i не превосходит весового остатка рюкзака. После чего он, предварительно обновив частичное решение, весовой остаток и суммарную стоимость предметов рюкзака, выполняет рекурсивный вызов с этими новыми параметрами и, сохранив результат в opt_v, завершается в строке 31 возвратом этого результата.

    Фнкция-оболочка knapsack_0_1_wrapper() инициализирует i значением 0, w_left - грузоподъёмностью рюкзака C и current_v - значением 0, поскольку рюкзак изначально пуст. Максимальное значение opt_v может быть нулём или некоторым отрицательным числом. На рисунке 1 мы посчитали его отрицательным с расчётом на то, что метод всё равно обновит его даже при пустом оптимальном решении (в крайнем левом листе).

    В заключение в примере 12.13 приведён простой итерационный код, который может использоваться для печати решения задачи.

def print_knapsack_solution(sol, w, v, C, opt_value):
    n = len(sol)
    k = 0
    while k < n and sol[k] == 0:
        k = k + 1

    total_weight = 0
    if k < n:
        print('(', w[k], ', ', v[k], ')', sep='', end='')
        total_weight = total_weight + w[k]

        for i in range(k + 1, n):
            if sol[i] == 1:
                total_weight = total_weight + w[i]
                print(' + ', sep='', end='')
                print('(', w[i], ', ', v[i], ')', sep='', end='')  

    print(' => ', '(', total_weight,
          ', ', opt_value, ')', sep='')


w = [3, 6, 9, 5]  # Список весов объектов
v = [7, 2, 10, 4]  # Список значений объектов
C = 15  # Грузоподъемность рюкзака
knapsack_0_1_wrapper(w, v, C)

    Стоимость решения можно вычислить по частичному решению и списку стоимостей предметов. Однако метод получает это значение в качестве параметра, так как оно возвращается функцией knapsack_0_1() и, следовательно, доступно в knapsack_0_1_wrapper(). В последних строках листинга алгоритму ставится конкретная задача, и он находит её решение.

    На следующем шаге мы рассмотрим алгоритм ветвей и границ.

Предыдущий шаг Содержание Следующий шаг