На этом шаге мы рассмотрим несколько заданий и приведем их решения.

Приведем несколько примеров решения задач.

Задание 1. Реализуйте алгоритм перебора с возвратами, который выводит все решения задачи n ладей. Он похож на задачу n ферзей, но вместо ферзей используются ладьи. Поскольку ладьи могут ходить только по вертикали и горизонтали, в каждой строке и каждом столбце может находиться только одна ладья. При этом на одной диагонали может стоять несколько ладей. На рисунке 1 приведено одно из решений задачи.

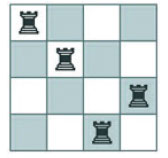
Рис.1. Одно из решений задачи четырёх ладей

Раскрыть/скрыть решение и комментарии.

В условии задачи сказано, что она похожа на задачу n ферзей. Воспользуемся этой подсказкой: уберем проверку диагоналей и добавим проверку столбцов (список free_cols). В остальном решение остается тем же самым.

Задача 1. Поиск всех решений задачи n ладей

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

def nrocks_all_sol(i, free_rows, free_cols,
                   sol):
    n = len(sol)

    # Проверка, является ли частичное решение полным
    if i == n:
        print_chessboard(sol)  # вывод решения
    else :

        # Генерация всех возможных вариантов,
        # которые могут бы быть представлены в частичном решении  
        for k in range(0, n):

            # Проверка, является ли
            # k-е решение валидным
            if free_rows[k] and free_cols[k]:
                # Помещение k-го кандидата в частичное решение
                sol[i] = k

                # Обновление структур данных, указывающее,
                # что k-й кандидат в частичном решении
                free_rows[k] = False
                free_cols[k] = False

                # Рекурсивный вызов, чтобы включить
                # больше кандидатов в частичное решение
                nrocks_all_sol(i + 1, free_rows, free_cols,
                               sol)

                # Исключение k-го кандидата из частичного
                # решения, и восстановление структур данных с
                # указанием того, что k-го кандидата больше
                # нет в частичном решении
                free_rows[k] = True
                free_cols[k] = True


def nrocks_wrapper(n):
    free_rows = [True] * n
    free_cols = [True] * n
    sol = [None] * n
    nrocks_all_sol(0, free_rows, free_cols, sol)


def print_chessboard(sol):
    for i in range(0, len(sol)):
        print(sol[i], ' ', end='')
    print()

Архив с файлом можно взять здесь.

Ниже приведен результат работы приложения для 4 ладей:

Задание 2. Магический квадрат - это сетка размером n*n, заполненная первыми n² положительными целыми числами так, что суммы чисел в каждой строке, столбце и диагонали одинаковы. Эта сумма называется "магической константой" и равна n(n² + 1)/2 для любого n. На рисунке 2 приведён пример магического квадрата размера 3*3 с магической константой 15.

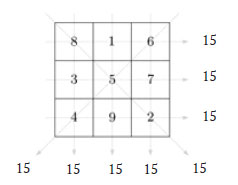
Рис.2. Магический квадрат 3*3

Разработайте алгоритм перебора с возвратами, который выводит все возможные магические квадраты размера 3*3. Примечание: разрабатывать алгоритм решения этой задачи для любого n не нужно. С какой проблемой можно столкнуться при решении этой задачи для бОльших значений n?

Раскрыть/скрыть решение и комментарии.

В этой задаче, по сравнению с предыдущей, нужно решить две проблемы.

Определиться, что проверять.
Как проверять.

Ответ на второй вопрос очевиден: проверяем равенство сумм по горизонталям, вертикалям и диагоналям "магической константе". Если все суммы равны этому значению, то получили магический квадрат и его выводим. В противном случае "откатываемся" для получения следующего варианта. Эта проверка реализована в функции magic_square_exam().

Ответ на первый вопрос тоже не слишком сложен. Создаем список списков (sol), заполненный нулями. Если очередной элемент равен 0, то помещаем на его место очередное значение (i), после чего пытаемся разместить следующее значение (i + 1).

Задача 2. Поиск всех решений задачи построения магического квадрата 3*3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

def magic_square_exam(sol, s):
    n = len(sol)

    # Проверка горизонталей
    for i in range(n):
        if sum(sol[i]) != s:
            return False

    # Проверка вертикалей
    arr = [True if sum(x) - s == 0 else False for x in zip(*sol)]
    if not all(arr):
        return False

    # Проверка главной диагонали
    a = sum([sol[i][i] for i in range(n)])
    if a - s != 0:
        return False

    # Проверка побочной диагонали
    a = sum([sol[i][n - i - 1] for i in range(n)])
    if a - s != 0:
        return False
    return True

def magic_all_sol(i, sol, s):
    n = len(sol)

    # Проверка, является ли частичное решение полным
    if magic_square_exam(sol, s):
        print_square(sol)  # вывод решения
    else:

        # Генерация всех возможных вариантов,
        # которые могут бы быть представлены в частичном решении
        for k_row in range(0, n):
            for k_col in range(0, n):

                # Проверка, является ли
                # k-е решение валидным
                if sol[k_row][k_col] == 0:

                    # Помещение k-го кандидата в частичное решение  
                    sol[k_row][k_col] = i

                    # Рекурсивный вызов, чтобы включить
                    # больше кандидатов в частичное решение
                    magic_all_sol(i + 1, sol, s)

                    # Исключение k-го кандидата из частичного
                    # решения, и восстановление структур данных с
                    # указанием того, что k-го кандидата больше
                    # нет в частичном решении
                    sol[k_row][k_col] = 0


def magic_square(n):
    sol = [0] * n
    s = n * (n * n + 1) / 2
    # Создаем список списков, заполненный нулями
    sol = [sol[:] for _ in range(n)]
    magic_all_sol(1, sol, s)


def print_square(sol):
    for i in range(len(sol)):
        print(*sol[i])
    print()

Архив с файлом можно взять здесь.

Ниже приведен результат работы приложения при n = 3 (magic_square(3)):

Мы разработали это приложение для любого n. Можно попытаться выполнить его при n = 4. Объяснение полученного результата оставляем за вами.

На этом мы заканчиваем наше знакомство с рекурсией и областями ее применения. Надеемся, что изложенный материал был Вам интересен и полезен. Удачи в освоении премудростей программирования!

Предыдущий шаг Содержание