На этом шаге рассмотрим трансформационные матрицы.
В каждом объекте класса QPainter хранится трансформационная матрица. Ее можно считать из него, а можно установить созданную матрицу трансформации с помощью метода QPainter::setMatrix(). Если для того чтобы получить нужный результат, вам необходимо вызывать несколько методов трансформации, то эффективнее записать их в объект матрицы и устанавливать ее в объекте QPainter всякий раз, когда необходима трансформация. Например:
QMatrix mat; mat.scale(2, 2); mat.shear(0.2, 0.5); mat.rotate(15); painter.setMatrix(mat); painter.drawText(rect(), Qt::AlignLeft, "Трансформация");
Результат применения трансформационной матрицы к тексту представлен на рисунке 1.
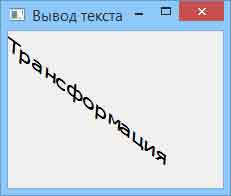
Рис.1. Пример трансформации текста
Файлы приложения можно взять здесь.
Любая двумерная трансформация может быть описана матрицей размерностью 3?3:
M11 M12 0
M21 M22 0
Dx Dy 0
Если стандартных трансформаций недостаточно, то можно определить свою собственную при помощи значений M11, M12, M21, M22, Dx и Dy, которые задаются в конструкторе класса QMatrix и представляют собой действительные числа. В табл. 1 сведены вместе основные формы трансформации в матричном представлении. Например, установка следующей матрицы в объекте QPainter будет соответствовать вызову его метода translate(20, 10):
QMatrix mat(1, 0, 0, 1, 20, 10); painter.setMatrix(mat);
Результат применения трансформационной матрицы к прямоугольнику представлен на рисунке 2.
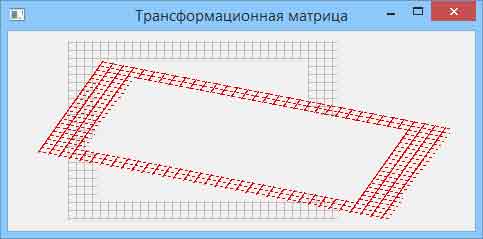
Рис.2. Пример трансформации прямоугольника
Файлы приложения можно взять здесь.
На следующем шаге рассмотрим отображение графической траектории.
