На этом шаге мы введем эти понятия.
Примеры предыдущего шага иллюстрируют некоторые особенности сетей Пери и систем, моделируемых с их помощью. Одной из особенностей является свойственный сетям и их моделям параллелизм или одновременность. В модели сети Петри два разрешенных невзаимодействующих события могут происходить независимо друг от друга. Синхронизировать события, пока это не требуется моделируемой системе, нет нужды. Но, когда синхронизация необходима, моделировать ее легко. Сети Петри представляются идеальными для моделирования систем с распределенным управлением, в которых несколько процессов выполняются одновременно.
Другая важная особенность сетей Петри - это их асинхронная природа. В сети Петри отсутствует измерение времени или течение времени. В реальной жизни различные события укладываются в различные интервалы времени, и это отражено в модели сети Петри независимостью от времени управления последовательностью событий. Структура сети Петри такова, что содержит в себе всю необходимую информацию для определения возможных последовательностей событий. Таким образом, на рисунке 2 предыдущего шага событие "завершение выполнения задания" должно следовать за соответствующим событием "начало выполнения задания". Однако нет и не требуется никакой информации, связанной с количеством времени, необходимым на выполнение задания.
Выполнение сети Петри рассматривается здесь как последовательность дискретных событий. Порядок появления событий является одним из возможных, допускаемых основной структурой. Это приводит к явной недетерминированности в выполнении сети Петри. Если в какой-то момент времени разрешено более одного перехода, то любой из нескольких возможных переходов может стать "следующим запускаемым". Выбор запускаемого перехода осуществляется недетерминированным образом, т.е. случайно. Эта особенность сети Петри отражает тот факт, что в реальной жизненной ситуации, где несколько действий происходит одновременно, возникающий порядок появления событий - не однозначен; скорее может возникнуть любая из множества последовательностей событий. Однако частичный порядок появления события - единственен.
Из теории относительности известно, что если два события произойдут одновременно (т.е. они не имеют причинной взаимосвязи), то порядок возникновения этих событий для двух разных наблюдателей может оказаться различным.
Такое представление влечет за собой значительные трудности при описании и анализе динамического поведения сети Петри, когда определяется последовательность запусков переходов. Для простоты обычно вводят следующее ограничение. Запуск перехода (и соответствующего события) рассматривается как мгновенное событие, занимающее нулевое время, и возникновение двух событий одновременно невозможно. Моделируемое таким образом событие называется примитивным; примитивные события мгновенны и неодновременны.
Непримитивными называются такие события, длительность которых отлична от нуля. Они не являются одновременными и, следовательно, могут пересекаться во времени.
Недетерминированность и неодновременность запусков переходов в моделировании параллельной системы показываются двумя способами. Один из них показан на рисунке 1.
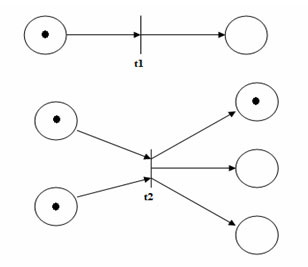
Рис.1. Одновременность
В этой ситуации два разрешенных перехода в любом случае не влияют друг на друга, и в число возможных последовательностей событий входит последовательность, в которой первым срабатывает один переход, и последовательность, в которой первым будет запушен другой переход. Это называется одновременностью.
Другая ситуация, в которой одновременное выполнение затруднено и которая характеризуется невозможностью одновременного возникновения событий, показана на рисунке 2.
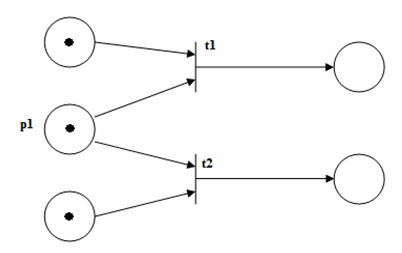
Рис.2. Конфликт
Здесь два разрешенных перехода находятся в конфликте. Может быть запущен только один переход, так как при запуске он удаляет фишку из общего входа и запрещает другой переход. Таким образом моделируются взаимоисключающие события системы.
Со следующего шага мы начнем рассматривать системы параллельных взаимодействующих процессов, моделируемых сетями Петри.
