На этом шаге мы приведем формулировку этой задачи.
Существует несколько вариантов задачи о чтении/записи, но основная их структура остается неизменной. Имеются процессы двух типов: процессы чтения и процессы записи. Все процессы совместно используют общий файл, переменную или элемент данных. Процессы чтения не изменяют объект в отличие от процессов записи. Таким образом процессы записи должны взаимно исключать все другие процессы чтения и записи, в то время, как несколько процессов чтения могут иметь доступ к разделяемым данным одновременно. Задача состоит в определении структуры управления, которая не приведет к тупику и не допустит нарушения критерия взаимного исключения.
На рисунке 1 иллюстрируется решение задачи в том случае, когда количество процессов чтения ограничено величиной n. Если в системе количество процессов не ограничено, то только n процессов могут выполняться в одно и то же время.
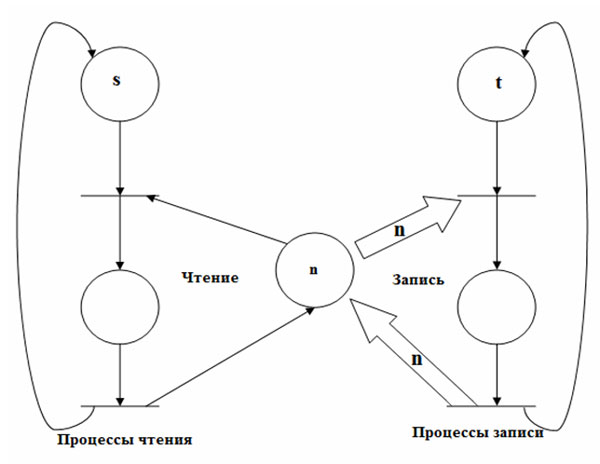
Рис.1. Задача о чтении/записи в случае, когда число процессов чтения ограничено величиной n
Проблема возникает в том случае, если количество процессов чтения не ограничено и предоставляется возможность неограниченному количеству процессов читать одновременно. В этом случае можно утверждать, что возникает необходимость хранения количества читающих процессов. При инициативе каждого процесса чтения в счетчик добавляется единица, а по окончании процесса единица вычитается. Это легко моделируется позицией, в которой количество фишек равно количеству процессов чтения. Однако, для того, чтобы предоставить процессу записи возможность приступить к записи, необходимо, чтобы счетчик был нулевым, т.е. соответствующая позиция была бы пустой. В сетях Петри нет механизма, который бы осуществлял проверку на нуль неограниченной позиции. Эта задача решается с помощью расширения модели сетей Петри.
На следующем шаге мы рассмотрим химические системы.
