На этом шаге мы рассмотрим начальные определения теории графов.
Граф (graph) - пара G=(V,E), где V - множество объектов произвольной природы, называемых вершинами (vertices, nodes), а E - семейство пар ei=(vi1, vi2), vij принадлежит V, называемых ребрами (edges). В общем случае множество V и/или семейство E могут содержать бесконечное число элементов, но мы будем рассматривать только конечные графы, т.е. графы, у которых как V, так и E конечны.
В приведенном определении графа E не случайно названо семейством пар, а не множеством. Дело в том, что элементы E могут быть неуникальны, т.е. возможны кратные ребра. Существует другое, более корректное определение: граф определяется как тройка G=(V,E,j), где V - множество вершин, E - множество ребер, а j=j(v,u,e) - трехместный предикат (булевская функция от трех переменных), возвращающая True тогда и только тогда, когда ребро e инцидентно вершинам v и u. Однако такие "строгости" в нашем изложении являются чрезмерными.
Если порядок элементов, входящих в ei, имеет значение, то граф называется ориентированным (directed graph), сокращенно - орграф (digraph), иначе - неориентированным (undirected graph). Ребра орграфа называются дугами (arcs). В дальнейшем будем считать, что термин "граф", применяемый без уточнений "ориентированный" или "неориентированный", обозначает неориентированный граф.
Пример: G=(V,E); V={1,2,3,4}; E=<(1,1), (1,2), (1,3), (2,4), (2,4)>.
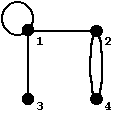
Рис.1. Пример графа
Если e=(v,u), то вершины v и u называются концами ребра. При этом говорят, что ребро e является смежным (инцидентным) каждой из вершин v и u. Вершины v и u также называются смежными (инцидентными). В общем случае, допускаются ребра вида e=(v,v); такие ребра называются петлями.
Степень вершины графа - это число ребер, инцидентных данной вершине, причем петли учитываются дважды. Поскольку каждое ребро инцидентно двум вершинам, сумма степеней всех вершин графа равна удвоенному количеству ребер: Sum(deg(vi), i=1..|V|)=2*|E|.
Граф, не содержащий петель и кратных ребер, называется обыкновенным, или простым графом (simple graph). Во многих публикациях используется другая терминология: под графом понимается простой граф, граф с кратными ребрами называют мультиграфом, с петлями - псевдографом.
Некоторые классы графов получили особые наименования. Граф с любым количеством вершин, не содержащий ребер, называется пустым. Обыкновенный граф с n вершинами, любая пара вершин которого соединена ребром, называется полным и обозначается Kn (очевидно, что в полном графе n(n-1)/2 ребер).
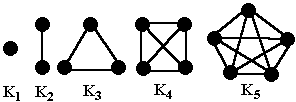
Рис.2. Примеры графов
Граф, вершины которого можно разбить на непересекающиеся подмножества V1 и V2 так, что никакие две вершины, принадлежащие одному и тому же подмножеству, не смежны, называется двудольным (или бихроматическим, или графом Кенига) и обозначается Bmn (m=|V1|, n=|V2|, m+n=|V|). Полный двудольный граф - такой двудольный граф, что каждая вершина множества V1 связана со всеми вершинами множества V2, и наоборот; обозначение - Kmn.
Замечание. Полный двудольный граф Bmn не является полным (за исключением B11=K2).
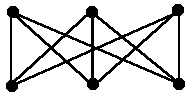
Рис.3. Двудольный граф
Подграфом, или частью графа G=(V,E) называется такой граф G'=(V',E'), что V' принадлежит V и две несмежные вершины в G не смежны в G'. Полным подграфом называется подграф, любая пара вершин которого смежна.
Остовным подграфом (суграфом) графа G называется любой его подграф, содержащий то же множество вершин, что и G.
На следующем шаге мы рассмотрим изоморфизм и гомеоморфизм графов.
