Шаг 4.
Основные понятия теории графов.
Деревья

    На этом шаге мы рассмотрим деревья.

    Деревом называется произвольный связный граф без циклов.

Лемма 1.

Пусть G=(V,E) - связный граф, вершины v₁ и v₂ которого не смежны. Тогда в графе G'=(V,E+(v₁,v₂)) существует простой цикл, проходящий через ребро (v₁,v₂).

Доказательство.

Т.к. G - связный, в нем существует путь из v₂ в v₁, а значит, и простая цепь v₂ ... v₁. Следовательно, в графе G' существует путь v₂ ...v₁(v₁,v₂) v₂, который является простым циклом (по определению).

Лемма 2.

Пусть G=(V,E) - связный граф, ребро e=(v₁,v₂) которого входит в некоторый цикл. Тогда граф G'=(V,E-e) - также связен, т.е. при удалении кольцевого ребра (ребра, входящего в некоторый цикл) из связного графа этот граф остается связным.

Доказательство.

Т.к. G - связный, в нем существует путь S между любыми двумя вершинами v_i и v_j. Если e не входит в путь S=v_i...v_j, то этот путь существует и в графе G', а значит, G' остается связным. Иначе (e входит в этот путь): S=v_i...v₁(v₁,v₂)v₂...v_j. По условию e входит в некоторый цикл, следовательно, существует замкнутый путь C=v₂(v₂,v₁)v₁Tv₂ (началом замкнутого пути мы можем считать любую его вершину), причем ребро e=(v₁,v₂) не входит в T (если существует путь между вершинами, то существует и путь, который является простой цепью). Но тогда существует путь S'=v_i...v₁Tv₂...v_j, в который не входит ребро e=(v₁,v₂) и, следовательно, этот путь существует в графе G'.

Лемма 3.

Пусть G=(V,E), p=|V|, q=|E|.

1. Число связных компонент в G больше либо равно |V|-|E| (N_комп.=p-q);
2. Если в G нет циклов, то число связных компонент в G равно |V|-|E| (N_комп.=p-q).

Доказательство.

Построим пустой граф с p вершинами (очевидно, в нем ровно p связных компонент) и будем добавлять ребра по одному.

    При добавлении ребра возможны две ситуации:

• а) новое ребро соединяет вершины, находившиеся до этого в разных компонентах (в этом случае количество компонент уменьшается на единицу) и
• б) новое ребро соединяет вершины, принадлежащие одной компоненте (число компонент не изменяется).

    Следовательно, при добавлении q ребер число компонент уменьшится не более чем на q, и, следовательно, количество компонент в графе будет больше либо равно p-q. Это доказывает утверждение (1).

    В соответствии с леммой 1, при добавлении ребра в связный граф в нем появляется цикл. Если в графе нет циклов, это означает, что при добавлении ребер всегда происходил вариант (а) - иначе появились бы циклы. Следовательно, число компонент при каждом добавлении ребра уменьшалось на единицу, и после добавления q ребер в графе будет ровно p-q компонент. Это доказывает утверждение (2).

Следствие 1 леммы 3.

Если |E|-|V|=2, то граф G=(V,E) несвязен (следует непосредственно из леммы 3).

Теорема 1.

Любой связный граф содержит подграф, являющийся деревом.

Доказательство.

Если в связном графе нет циклов, то он уже является деревом по определению. Иначе находим любое кольцевое ребро и удаляем его; в соответствии с леммой 2 граф остается связным. Продолжаем процесс, пока в графе существуют циклы. В силу конечности графа этот алгоритм построит дерево за конечное число шагов.

---

    Замечание. Фактически доказано более сильное утверждение - что любой связный граф содержит остовный подграф (подграф с тем же количеством вершин, что и сам граф), являющийся деревом.

---

Теорема 2.

Для любого дерева G=(V,E) верно: |V|-|E|=1.

Доказательство.

По определению, в дереве нет циклов, следовательно, в соответствии с леммой 3 в нем ровно |V|-|E| связных компонент. Но по определению дерево связно, т.е. состоит из одной связной компоненты, поэтому |V|-|E|=1.

Теорема 3.

Следующие свойства графов эквивалентны:

1. G=(V,E) - дерево.
2. Любые две вершины G соединены единственной простой цепью.
3. G - граф без циклов, у которого |E|=|V|-1.
4. G - связный граф, у которого |E|=|V|-1.
5. G - связный граф, но при удалении любого ребра он становится несвязным.
6. G - граф без циклов, но при добавлении любого ребра в нем появляется ровно один (с точностью до задания начальной вершины и направления обхода) простой цикл.

Доказательство.

Докажем теорему в последовательности (1)<=>(2), (2)=>(3)=>(4)=>(5)=>(6)=>(1).

    (1)=>(2): допустим, что некоторые две вершины v₁ и v₂ графа G соединены, по крайней мере, двумя различными простым цепями L₁=u₁...u_k, где u₁=v₁ и u_k=v₂, и L₂=w₁....w_m, где w₁=v₁ и w_m=v₂. Из того, что цепи являются простыми и различными, следует, что существует число j, 1<j<min(k,m), такое, что u_j-1=w_j-1, u_jw'_j, ... , u_j+a-1w'_j+b-1, u_j+a=w_j+b, где a=1, b=1. Следовательно, в G существует цикл С=u_j-1(u_j-1,u_j)u_j...u_j+a(w_j+b,w_j+b-1)w_j+b-1... w_j(w_j,w_j-1)w_j-1 (см. рисунок) - получили противоречие с (1).

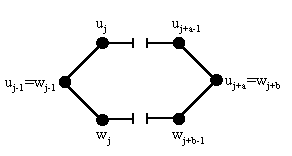
Рис.1. Иллюстрация к (1)=>(2)

    (2)=>(1):

    (а) граф G является связным по определению связности (любые две вершины графа соединены цепью);

    (б) допустим, что в графе G существует цикл, проходящий через некоторую вершину v: C=v(v,u₁)u₁....u_k(u_k,v)v. Но это означает, что между v и любой из вершин u_i существуют, по крайней мере, два различных пути L₁=v(v,u₁)u₁...u_i-1(u_i-1,u_i)u_i и L₂=v(v,u_k)u_k...u_i+1(u_i+1,u_i)u_i (пути различны, т.к. по определению в цикле отсутствуют повторяющиеся ребра). В силу утверждения 1 из этих путей можно "выделить" простые цепи, которые также будут различны (в L₁и L₂ нет совпадающих ребер), - получили противоречие с (2).

    Из (а), (б) и определения дерева следует, что G является деревом.

    (2)=>(3): по теореме 2;

    (3)=>(4): по лемме 3;

    (4)=>(5): т.к. |E|=|V|-1, то после удаления ребра в новом графе будет |V|-2 ребер, и по следствию 1 леммы 3 этот граф будет несвязным;

    (5)=>(6):

    (a) докажем первую часть утверждения (G - граф без циклов): допустим, в G есть циклы; но тогда при удалении любого кольцевого ребра он останется связным, что противоречит (4);

    (b) докажем вторую часть утверждения (при добавлении любого ребра в G появляется ровно один простой цикл): из связности графа и леммы 1 следует, что при добавлении любого ребра в G появляется, как минимум, один простой цикл; в силу (2) этот простой цикл единственен (обратное означало бы, что в G существуют вершины, соединенные более чем одной простой цепью);

    (6)=>(1): допустим, G - не дерево, т.е. граф не связен или содержит циклы. Циклов не может быть в силу (5а), поэтому остается вариант: G - несвязен и состоит минимум из двух компонент. Но тогда при добавлении ребра между вершинами, принадлежащими разным компонентам, циклы не образуются, а это противоречит (5б).

    Остовным деревом (остовом) связного графа называется любой его остовный подграф, являющийся деревом.

    Существование остовного подграфа для любого связного графа доказывается теоремой 1.

    Общее число остовных деревьев связного графа может быть весьма велико. Так, для полного графа с n вершинами оно равно n^n-2 (без доказательства).

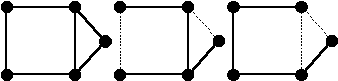
Рис.2. Граф и два его остовных дерева (удаленные ребра показаны пунктиром)

    Для произвольного (возможно, несвязного) графа G остовное дерево определяется как любой его остовный подграф, не содержащий циклов и имеющий столько же компонент связности, что и G.

    На следующем шаге мы рассмотрим цикломатическое число и фундаментальные циклы.

Предыдущий шаг Содержание Следующий шаг