На этом шаге мы рассмотрим поиск в глубину.

Многие алгоритмы на графах основаны на систематическом переборе всех вершин графа, при котором каждая вершина просматривается в точности один раз. Здесь мы рассмотрим два стандартных и широко используемых метода такого перебора: поиск в глубину и поиск в ширину. Оба метода изучаются применительно к обыкновенным графам, поскольку на произвольные графы они могут быть распространены очевидным образом. Поиск в глубину применяется для отыскания компонент сильной связности в орграфе.

Поиск в глубину

Идея этого метода состоит в следующем. Поиск в обыкновенном графе G начинается с некоторой начальной вершины v (с этого момента v считается просмотренной). Пусть m - последняя просмотренная вершина (этой вершиной может быть и v). Тогда возможны два случая.

Среди вершин, смежных с m, существует еще непросмотренная вершина w. Тогда m объявляется просмотренной, и поиск продолжается из вершины w. Будем говорить, что вершина m является отцом вершины w (m = father[w]). Ребро mw в этом случае будет называться древесным.
Все вершины, смежные с m, просмотрены. Тогда m объявляется использованной вершиной. Обозначим через x ту вершину, из которой мы попали в m, т.е. x = father[m]; поиск в глубину продолжается из вершины х.

Что произойдет, когда все просмотренные вершины будут использованы? Если в графе G не осталось непросмотренных вершин, то поиск заканчивается. Если же осталась непросмотренная вершина y, то поиск продолжается из этой вершины.

Поиск в глубину просматривает вершины графа G в определенном порядке. Для того чтобы зафиксировать этот порядок, будет использоваться массив num[v]. При этом естественно считать, что num[v] = 1, если v начальная вершина, и num[w] = num[m] + 1, если w просматривается сразу после того, как просмотрена вершина m.

Пусть в обыкновенном графе G проведен поиск в глубину. Обозначим через Т множество всех древесных ребер. Все остальные ребра графа будем называть обратными ребрами. Множество всех обратных ребер будем обозначать через В.

Результат применения поиска в глубину к связному графу G (рисунок 1а) показан на рисунке 1б. Здесь сплошные линии изображают древесные ребра, а пунктирные линии - обратные ребра. Заметим, что нумерация вершин соответствует порядку, в которым они просматриваются поиском в глубину. Можно обратить внимание на то, что множество всех древесных ребер с выделенной начальной вершиной v₁ образует корневое дерево с корнем v₁. Это корневое дерево часто называют глубинным деревом, или, короче, d-деревом графа G. Следует также отметить, что каждое обратное ребро соединяет в d-дереве предка и потомка.

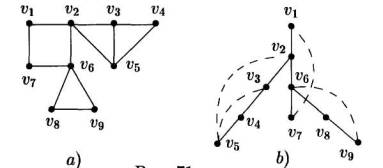
Рис.1. Обход графа

Пусть G - несвязный граф, G₁, ..., G_k - множество всех его компонент связности. Обозначим через Т_i множество древесных ребер, выделенных поиском в глубину в компоненте G_i, а через v_i - корневую вершину из G_i, т.е. первую просмотренную вершину подграфа G_i. Таким образом, множество всех древесных ребер несвязного графа образует остовный лес. Фиксируя в каждом поддереве этого леса корневую вершину, мы получим глубинный лес или, короче, d-лес графа G.

Представим теперь формальное описание указанного алгоритма. В алгоритме используются описанные ранее массивы num и father. В процессе работы алгоритма массив num используется для распознавания непросмотренных вершин, а именно, равенство num[v] = 0 означает, что вершина v еще не просмотрена.

Вначале изложим версию алгоритма поиска в глубину, основанную на рекурсивной процедуре DFS(v) (название процедуры является аббревиатурой от англ. depth first search), осуществляющей поиск в глубину из вершины v.

Алгоритм 1.

1. procedure DFS(v);
2.  begin
3.      num[v]:= i; i:= i + 1;
4.      for u ∈ list[v]   do
5.         if num [u] = 0 then
6.             begin
7.                  T:= T ∪ {uv}; father[u]:= v; DFS(u)
8.             end
9.         else 
10.           if num[u] < num[v] and u ≠ father[v] 
11.           then
12 .               B:= B ∪ {uv}
13. end;
14. begin
15.     i:= 1; T:= 0; В:= 0;
16.     for v ∈ V   do  num[v]:= 0;
17.       for v ∈ V do
16.          if num[v] = 0 then
17.             begin
18.                 father[v]:= 0; DFS(v);
19.             end
20. end.

Алгоритм 1 применим к произвольному обыкновенному графу G. Если G - связный граф, то цикл достаточно заменить вызовом процедуры DFS(v_q) применительно к начальной вершине v_q. Заметим, что в терминах алгоритма 1 вершина v просмотрена с началом работы процедуры DFS(v); в тот момент, когда процедура DFS(v) закончила работу, вершина v является использованной.

Теорема 1.

Пусть G - связный (n, m)-граф. Тогда

поиск в глубину просматривает каждую вершину в точности один раз;
поиск в глубину требует O(n + m) операций;
подграф (V, Т) графа G является деревом.

Доказательство.

Проверка в строке 5 гарантирует, что каждая вершина просматривается не более одного раза. Убедимся, что поиск в глубину просматривает каждую вершину. Пусть X - множество просмотренных вершин в тот момент, когда алгоритм закончил работу, Y = V\X. Если Y непусто, то в силу связности графа G существует такое ребро ху, что х ∈ X, у ∈ Y. Процедура DFS(x) полностью проработала, поэтому смежная с x вершина y должна быть просмотрена. Получили противоречие.
Число повторений цикла в процедуре (начало цикла в строке 4) с учетом рекурсивных обращений равно сумме степеней всех вершин графа, т. е. оно равно 2m; следовательно, число операций пропорционально m. Число повторений цикла в строке 14, очевидно, пропорционально n. Отсюда вытекает, что поиск в глубину требует О(n + m) операций.
Ясно, что условие num[u] = 0 (строка 5) выполнится n-1 раз. Отсюда следует, что |Т| = n-1. Кроме того, из 1) вытекает, что множество ребер Т не содержит циклов. Таким образом, граф (V, Т) ацикличен и число ребер в этом графе на единицу меньше числа вершин. Следовательно, граф (V, Т) - дерево.

Пусть G - связный граф, v₀ - некоторая его вершина. Предположим, что в графе G проведен поиск в глубину из вершины v_q. Дерево (V, Т) с выделенной вершиной v_q является корневым деревом. Как отмечалось выше, это корневое дерево часто называют d-деревом или глубинным деревом графа G. Для любой вершины u≠v₀ вершина father[u] является отцом и в d-дереве.

Рассмотрим нерекурсивную версию процедуры DFS(v). Рекурсия устраняется при помощи стека S, элементами которого являются вершины графа. Вершина v является просмотренной, если num[v]≠0. Вершина v становится использованной с момента, когда v - top(S) (v находится в вершине стека) и все вершины, смежные с v, уже просмотрены (в этом случае v удаляется из стека). Вычисления, связанные с множеством обратных ребер B, здесь опущены; разобравшись с рекурсивной версией процедуры DFS(v), без труда можно восстановить их.

1. procedure DFS(v);
2. begin
3.    num[u]:= i; i:= i+1;
4.    S:= nil; S <= v;
5.    while S ≠ nil do
6.    begin
7.      v:= top(S);
8.      if exists u, u ∈ list[v] and num[u] = 0
9.      then
10.       begin
11.           num[u]:= i; i:= i + 1; T:= T ∪ {uv};
12.           father[u]:= v; S<= v
13.       end
14.     else v <= S
15.   end
16. end;

Отметим следующее важное свойство поиска в глубину: если xy - обратное ребро, то вершины x, y сравнимы в d-дереве, т.е. одна из этих вершин является предком другой.

В самом деле, пусть xy - обратное ребро графа G, причем num[x] < num[y]. Предположим, что вершины x и y несравнимы в d-дереве. Из описания алгоритма 1 следует, что в промежуток времени между началом работы процедуры DFS(x) и ее завершением, будут просмотрены только потомки этой вершины. Поскольку y ∈ list[v] и в момент завершения процедуры DFS(x) вершина y еще не просмотрена, получаем противоречие с описанием алгоритма 1.

На следующем шаге мы рассмотрим алгоритм отыскания блоков и точек сочленения.

Содержание Следующий шаг