На этом шаге мы рассмотрим алгоритм отыскания эйлеровой цепи в эйлеровом графе.
Напомним, что замкнутая цепь в графе G называется эйлеровой, если она содержит все ребра и все вершины графа. Связный неодноэлементный граф эйлеров тогда и только тогда, когда каждая его вершина имеет четную степень.
Этот шаг посвящен построению и анализу алгоритма, позволяюющего в связном обыкновенном графе G с четными степенями вершин построить эйлерову цепь. В алгоритме используются два стека SWork и SRes; элементами обоих стеков являются вершины графа G. Кроме того, введен массив listW, элементы которого - списки вершин. Мы считаем, что для каждой вершины v начальное значение listW[u] совпадает со списком всех вершин, смежных с вершиной v, т.е. с list(v).
Алгоритм 5.
Вход: связный граф G = (V, Е) без вершин нечетной степени, начальная вершина v0.
Выход: эйлерова цепь, представленная последовательностью вершин в стеке SRes.
1. begin 2. SWork:= nil, SRes:= nil; 3. SWork <= v0; 4. for v ∈ V do listW[v]:= list[v]; 5. while SWork ≠ nil do 6. begin 6. v:= top(SWork); 7. if listW(v) ≠ 0 then 9. begin 8. u:=первая вершина listW(v); 9. SWork <= u 10. listW(v):= listW(v)\{u}; 11. listW(u):= UstW(u)\{v}; 14. end 15. else 16. begin v <= SWork; SRes <= v; end 17. end 18. end.
Принцип работы этого алгоритма состоит в следующем. Алгоритм начинает работу с некоторой вершины v0 продвигаться по ребрам графа, причем каждое пройденное ребро из графа удаляется (строки 10-13). Ясно, что последовательное выполнение этой группы операторов позволяет выделить в графе некоторую замкнутую цепь. Затем начинается выполнение группы операторов из строки 16. Эти операторы выталкивают очередную вершину из стека SWork в стек SRes до тех пор, пока не выполнится одно из условий:
- стек SWork пуст (алгоритм заканчивает работу);
- для вершины v = top(SWork) существует непройденное ребро vu. В этом случае алгоритм продолжает работу из вершины u.
На рисунке 1 изображен эйлеров граф и эйлерова цепь, построенная алгоритмом 5 (предполагается, что все списки вершин упорядочены по возрастанию номеров).
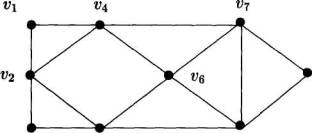
Рис.1. Эйлеров граф и эйлерова цепь
- Теорема 8.
- Алгоритм 5 правильно строит эйлерову цепь в эйлеровом графе G.
- Доказательство.
- Заметим сначала, что из стека SRes вершины никогда не выталкиваются. Отсюда следует, что, начиная с
некоторого момента работы алгоритма, стек SRes перестанет изменяться. Это произойдет после выполнения
операторов в строке 16. Предположим, что стек SWork в этот момент непуст. Если v = top(SWork),
операторы в строках 10-13 начнут добавлять вершины к стеку SWork (это означает, что в графе G из вершины v можно
построить цепь, состоящую из еще непройденных ребер). Ясно, что построение такой цепи должно прекратиться.
Это означает, что мы придем в вершину u, для который все инцидентные ей ребра уже пройдены (UstW(u) = 0). После
этого начнут выполняться операторы из строки 16, и, следовательно, к стеку SRes добавится хотя бы одна
вершина, что невозможно. Таким образом, стек SWork рано или поздно обязательно станет пустым,
что приведет к завершению работы алгоритма.
Пусть P - цепь, содержащаяся в стеке SRes после окончания работы алгоритма. Легко понять, что вершина w помещается в стек SRes, если все ребра, инцидентные с w, уже пройдены. Отсюда следует, что для любой вершины цепи P все ребра, инцидентные этой вершине, содержатся в цепи P. Поскольку G - связный граф, цепь P содержит все ребра графа G. Теперь легко понять, что P - эйлерова цепь.
В заключение оценим сложность алгоритма 5. Для этого заметим, что при каждой итерации цикла либо к стеку SWork добавляется вершина (это означает прохождение очередного ребра), либо вершина переносится из стека SWork в SRes (другими словами к строящейся эйлеровой цепи добавляется ребро). Отсюда следует, что число повторений цикла равно O(m). Если позаботиться о том, чтобы время, необходимое для удаления вершины из списка HstW[v], было ограничено константой, то сложность алгоритма 5 будет равна O(m).
На следующем шаге мы рассмотрим задачу о минимальном остове.
