На этом шаге мы рассмотрим алгоритм Ярника - Прима - Дейкстры.
Перейдем к рассмотрению алгоритма Ярника - Прима - Дейкстры, основанного на применении стратегии 2. Впервые он появился в работе Ярника, опубликованной в 1930 году, затем был переоткрыт Примом в 1957 году и независимо Дейкстрой в 1959 году. Заметим, что Дейкстра предложил очень эффективную реализацию этого алгоритма, связанную с расстановкой специальных меток.
Для ребра е = vw вес c(е) будет иногда обозначаться через c(v, w). Напомним, что в обсуждаемом алгоритме строится последовательность (3), состоящая из деревьев, в которой дерево Hi получается из Hi-1 поглощением ближайшей к дереву Нi-1 вершины. Для организации эффективного выбора такой вершины используются два массива: near[v] и d[v]. Пусть Н - произвольное дерево из последовательности (3), U - множество его вершин. По определению d[v] равно расстоянию от вершины v до множества U, иными словами
d[v] = min{c(v, u) | u ∈ U}.
Пусть d[v] = c(v, w), w ∈ U. Тогда near[v] = w. Иными словами, near[v] - ближашая к v вершина из множества U.
Пусть W = V\U. Будем считать, что если vw ∉ Е, то c(v, w) - ∞. Через Min(W) обозначим функцию, значением которой является вершина v ∈ W, имеющая минимальное значение метки d.
Алгоритм 2 (Ярник, Прим, Дейкстра).
Вход: связный взвешенный граф G = (V, Е, с), заданный матрицей весов А[1... n, 1... n].
Выход: минимальный остов Т графа G.
1. begin 2. w:= произвольная вершина из V; 3. W:= V\{w}; T:= ∅; 4. for v ∈ V do 5. begin 6. near[v]:= w; d[v]:= A[v, w] 7. end; 8. while |T| ≠ n-1 do 9. begin 10. v:= Min(W); u:=near[v]; 11. T:=T ∪ {vu};W:=W\{v}; 12. for u ∈ W do 13. if d[u] > A[u, v] then 14. begin 15. near[u]:= v; d[u] - A[u, v]; 16. end 17. end 18. end.
- Теорема 2.
- Алгоритм Ярника - Прима - Дейкстры применительно к связному взвешенному (n, m)-графу имеет сложность O(n2).
- Доказательство.
- Каждый проход цикла в строках 8-17 уменьшает на единицу число вершин во множестве W. После k проходов цикла 8-17 множество
W будет содержать n-k вершин. Следовательно, число операций, необходимых для выбора вершины Min(W), пропорционально
n-k (строка 10). В строках 12-16 осуществляется пересчет меток для n-k-1 вершин, т.е. число операций в цикле 12-16 пропорционально n-k-1.
Окончательно, число операций в алгоритме 2 пропорционально сумме
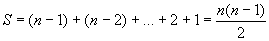
имеющей, порядок n2, что и доказывает теорему.
Проиллюстрируем работу алгоритма 2 на графе, изображенном на рисунке 1.

Рис.1. Связный граф и минимальный остов
Здесь в качестве вершины w выбрана вершина v1.
| |T| | U=V \ W | Near | d |
|---|---|---|---|
| v2, v3, v4, v5, v6 | v2, v3, v4, v5, v6 | ||
| 0 | v1 | v1, v1, v1, v1, v1 | 2, 3, 4, ∞, ∞ |
| 1 | v1, v2 | v1, v2, v1, v1 | 3, 3, ∞, ∞ |
| 2 | v1, v2, v3 | v3, v3, v3 | 2, 4, 5 |
| 3 | v1, v2, v3, v4 | v3, v4 | 4, 4 |
| 4 | v1, v2, v3, v4, v5 | v5 | 2 |
| 5 | v1, v2, v3, v4, v5, v6 |
В результате работы алгоритма получится остов
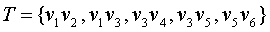
Ребра остова перечислены в том порядке, в каком они были найдены. Этот остов изображен на рисунке 1б), т.е. он совпадает с остовом, построенным алгоритмом Борувки-Краскала. Заметим, что функция Min(W) при наличии нескольких претендентов выбирала тот, у которого номер меньше. Например, в третьей строке таблицы вершине v3 отдано предпочтение перед вершиной v4. Аналогичная ситуация в предпоследней строке.
В научной литературе имеется много работ, посвященных различным вариантам постановки задачи о минимальном остове. Например, совсем недавно разработан алгоритм построения минимального остова в евклидовом графе, имеющий сложность O(n log n). Здесь под евклидовым графом понимается полный граф, вершинами которого являются точки n-мерного евклидова пространства, а вес каждого ребра равен расстоянию между его концами. Задача о минимальном остове для евклидовых графов на плоскости (случай n=2) находит непосредственное применение при проектировании радиоэлектронных изделий.
Дополнительный материал по этим вопросам можно взять здесь.
