На этом шаге мы рассмотрим вероятностное динамическое программирования.

Выделяют два вида динамического программирования: детерминированное и вероятностное. [1, c 562].

Вероятностное динамическое программирование отличается от детерминированного динамического программирования тем, что состояния и прибыли на каждом этапе являются случайными. Модели вероятностного динамического программирования возникают, в частности, при рассмотрении стохастических моделей управления запасами и в теории марковских процессов принятия решений.

Чтобы лучше понять отличие вероятностного динамического программирования от детерминированного динамического программирования рассмотрим алгоритм решения задачи "Азартная игра". Она является ярким примером решения задачи с помощью вероятностного динамического программирования.

Задача "Азартная игра"

Одна из разновидностей игры в русскую рулетку состоит во вращении колеса, на котором по его периметру нанесены n последовательных чисел от 1 до n. Вероятность того, что колесо в результате одного вращения остановится на цифре i, равна p_i. Игрок платит x долларов за возможность осуществить m вращений колеса. Сам же игрок получает сумму, равную удвоенному числу, которое выпало при последнем вращении колеса. Поскольку игра повторяется достаточно много раз (каждая до m вращений колеса), требуется разработать оптимальную стратегию для игрока [1, с. 562].

Сформулируем задачу в виде модели динамического программирования, используя следующие определения.

Этап i соответствует i-му вращению колеса, i = 1,2,..., m.
Альтернативы на каждом этапе состоят в следующем — либо покрутить колесо еще раз, либо прекратить игру.
Состояние системы j на каждом этапе i представляется одним из чисел от 1 до n, которое выпало в результате последнего вращения колеса.

Пусть f_i( j ) — максимум ожидаемой прибыли при условии, что игра находится на этапе (вращении) i и исходом последнего вращения есть число j. Ожидаемая прибыль на этапе i при условии, что исходом последнего вращения есть j, равна:

2j, если игра заканчивается;
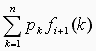, если игра продолжается.

Рекуррентное уравнение для f_i( j ) можно записать следующим образом:

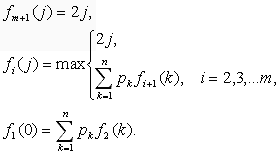
Обоснование рекуррентного уравнения сводится к следующему:

При первом вращении колеса (i = 1) состоянием системы является j = 0, ибо игра только началась. Следовательно, f₁( 0 ) = p₁f₂( 1 ) + p₂f₂( 2 ) + ... +p_nf₂( n ). После выполнения последнего вращения колеса (i = m) имеется лишь один выбор - закончить игру независимо от исхода j m-го вращения. Следовательно, f_m+1( j ) = 2j.

Рекуррентные вычисления начинаются с f_m+1, заканчиваются при f₁( 0 ) и сводятся, таким образом, к m+1 вычислительному этапу. Так как f₁( 0 ) представляет собой ожидаемую прибыль от всех m вращений колеса, а игра обходится игроку в x долларов, имеем следующее: ожидаемая прибыль равна f₁( 0 ) - x.

Таким образом, алгоритм решения этой задачи составлен. Надеюсь, вы поняли что такое вероятностное динамическое программирование. В дальнейшем мы будем рассматривать только детерминированное динамическое программирование.

⁽¹⁾ Хэмди А. Таха. Введение в исследование операций, 6-е издание.: Пер. с англ. — М.: Издательский дом "Вильямс", 2001. - 912с.: ил.

На следующем шаге мы выясним когда же все-таки применяется динамическое программирование.

Предыдущий шаг Содержание Следующий шаг