Здесь мы разберем решение задачи "Перемножение нескольких матриц".
Дана последовательность из n матриц заданных размеров [A1, A2, ..., An] (матрица Ai имеет размер pi-1 на pi ); требуется найти такую (полную) расстановку скобок в произведении A1A2 ... An, чтобы вычисление произведения требовало наименьшего числа умножений и найти результат перемножения этих матриц. [1, с.289].
Нужно найти произведение
A1A2 ... An(1)
последовательности n матриц . Будем пользоваться стандартным алгоритмом перемножения двух матриц в качестве подпрограммы. Но прежде надо расставить скобки в произведении матриц (1), чтобы указать порядок умножений. Будем говорить, что в произведении матриц полностью расставлены скобки, если это произведение либо состоит из одной единственной матрицы, либо является заключенным в скобки произведением двух произведений с полностью расставленными скобками. Поскольку умножение матриц ассоциативно, конечный результат вычислений не зависит от расстановки скобок. Например, в произведении A1A2A3A4 можно полностью расставить скобки пятью разными способами: (A1(A2(A3A4)))), (A1((A2A3)A4)), ((A1A2)(A3A4)), ((A1(A2A3))A4), ((((A1A2)A3)A4) - во всех случаях ответ будет один и тот же.
Не влияя на ответ, способ расстановки скобок может сильно повлиять на стоимость перемножения матриц. Посмотрим сначала, сколько операций требует перемножение двух матриц. Cтандартный алгоритм можно посмотреть здесь (rA, rB и cA, cB обозначают количество строк и столбцов матриц соответственно).
Матрицы A и B можно перемножать, только если число столбцов у A равно числу строк у B. Если A - это (p*q) - матрица, а B - это (q*r) - матрица, то их произведение С является (p*r) - матрицей. При выполнении этого алгоритма делается pqr умножений и примерно столько же сложений. Для простоты мы будем учитывать только умножения.
Рассмотрим решение этой задачи поэтапно, согласно шагу 2.
Этап 1: строение оптимальной расстановки скобок
Для того чтобы воспользоваться динамическим программированием, сначала нужно описать строение оптимальных решений. Для задачи об умножении последовательности матриц это выглядит следующим образом. Обозначим для удобства через Ai..j матрицу, являющуюся произведением AiAi+1 ... Aj. Оптимальная расстановка скобок в произведении A1A2 ... An разрывает последовательность между A1..k и Ak+1..n для некоторого k, удовлетворяющего неравенству 1 ≤ k < n. Иными словами, при вычислении произведения, диктуемом этой расстановкой скобок, мы сначала вычисляем произведения A1..k и Ak+1..n, а затем перемножаем их и получаем окончательный ответ A1..n. Стало быть, стоимость этой оптимальной расстановки равна стоимости вычисления матрицы A1..k плюс стоимость вычисления матрицы Ak+1..n плюс стоимость перемножения этих двух матриц.Чем меньше умножений потребуется для вычисления A1..k и Ak+1..n, тем меньше будет общее число умножений. Стало быть, оптимальное решение задачи о перемножении последовательности матриц содержит оптимальные решения задач о перемножении ее частей. Это и позволит применить динамическое программирование.
Этап 2: рекуррентное соотношение
Теперь надо выразить стоимость оптимального решения задачи через стоимости оптимальных решений ее подзадач. Такими подзадачами будут задачи об оптимальной расстановке скобок в произведениях Ai..j для 1 ≤ i ≤ j ≤ n. Обозначим через m[i, j] минимальное количество умножений, необходимое для вычисления матрицы Ai..j, в частности, стоимость вычисления всего произведения A1..n есть m[1, n].Числа m[i, j] можно вычислить так. Если i = j, то последовательность состоит из одной матрицы Ai..i=Ai и умножения вообще не нужны. Стало быть, m[i, i] = 0 для i = 1,2,...,n. Чтобы подсчитать m[i, j] для i < j, воспользуемся информацией о строении оптимального решения, полученной на этапе 1. Пусть при оптимальной расстановке скобок в произведении Ai..j последним идет умножение Ai..k на Ak+1..j, где 1 ≤ k < n. Тогда m[i, j] равно сумме минимальных стоимостей вычисления произведений Ai..k и Ak+1..j плюс стоимость перемножения этих двух матриц. Поскольку для вычисления произведения Ai..kAk+1..j требуется pi-1pkpj умножений, то m[i, j] = m[i, k] + m[k+1, j] + pi-1pkpj.
В этом соотношении подразумевается, что оптимальное значение k известно; на деле это не так. Однако число k может принимать всего лишь j-i различных значений: i, i+1, ...,j-1. Поскольку одно из них оптимально, достаточно перебрать эти значения k и выбрать наилучшее. Получаем рекуррентную формулу:
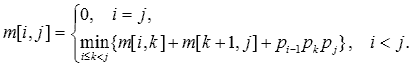 (2)
(2)
Числа m[i, j] – стоимости оптимальных решений подзадач. Чтобы проследить за тем, как получается оптимальное решение, обозначим через s[i, j] оптимальное место последнего умножения, то есть такое k, что при оптимальном вычислении произведения Ai..j последним идет умножение Ai..k на Ak+1..j. Иными словами, s[i, j] равно числу k, для которого m[i, j] = m[i, k] + m[k+1, j] + pi-1pkpj.
Этап 3: вычисление оптимальной стоимости
Пользуясь соотношениями (2), можно написать рекурсивный алгоритм, определяющий минимальную стоимость вычисления произведения A1..n(то есть число m[1, n]). Однако время работы такого алгоритма экспоненциально зависит от n, так что этот алгоритм не лучше полного перебора. Настоящий выигрыш во времени получим, если воспользуемся тем, что подзадач относительно немного: по одной задаче для каждой пары (i, j), для которой 1 ≤ i ≤ j ≤ n. Экспоненциальное время работы возникает потому, что рекурсивный алгоритм решает каждую из подзадач несколько раз, на разных ветвях дерева рекурсии.Вместо рекурсии вычислим оптимальную стоимость «снизу вверх». В программе предполагается, что матрица A1 имеет размер pi-1*pi при i =1,2,...,n. На вход подается последовательность P = {p0, p1,...,pn}. Программа использует вспомогательные таблицы m[1..n, 1..n] (для хранения стоимостей m[i, j]) и s[1..n, 1..n] (в ней отмечается, при каком k достигается оптимальная стоимость при вычислении m[i, j]).Этот алгоритм можно посмотреть здесь.
Заполняя таблицу m, алгоритм последовательно решает задачи об оптимальной расстановке скобок для одного, двух, ..., n сомножителей. В самом деле, соотношение (2) показывает, что число m[i, j] - стоимость перемножения j-i+1 матриц - зависит только от стоимостей перемножения меньшего числа матриц. Именно, для k = i, i+1,..., j-1 получается, что Ai..k - произведение k - i + 1 < j - i + 1 матриц, a Ak+1..j - произведение j - k < j - i + 1 матриц.
Сначала алгоритм выполняет присваивания m[i, i]:= 0 для i = 1,2, ...,n: стоимость перемножения последовательности из одной матрицы равна нулю. При первом исполнении цикла вычисляются (с помощью соотношений (2)) значения m[i, i + 1] для i = 1,2, ...,n-1 – это минимальные стоимости для последовательностей длины 2. При втором проходе вычисляются m[i, i + 2] для i = 1,2, ...,n-2 – минимальные стоимости перемножения последовательностей длины 3, и так далее. На каждом шаге значение m[i, j] зависит только от вычисленных ранее значений m[i, k] и m[k+1, j]. Так как ищем минимальную стоимость перемножения, то при каждом повторении цикла m[i, j] присваиваем максимально возможное значение, а так как элементы в таблице m имеют тип integer, то максимально возможное число равно maxint. Затем сравниваем это значение с полученной стоимостью и, таким образом, находим минимальное значение.
Простая оценка показывает, что время работы алгоритма MATRIX_CHAIN_ORDER есть O(n3). В самом деле, число вложенных циклов равно трем, и каждый из индексов l, i и k принимает не более n значений. Тем самым этот алгоритм значительно эффективнее, чем требующий экспоненциального времени перебор всех расстановок.
Этап 4: построение оптимального решения
Алгоритм MATRIX_CHAIN_ORDER находит минимальное число умножений, необходимое для перемножения последовательности матриц. Осталось найти расстановку скобок, приводящую к такому числу умножений.Для этого используем таблицу s[1.. n, 1.. n]. В клетке s[1,n] записано место последнего умножения при оптимальной расстановке скобок; другими словами, при оптимальном способе вычисления A1..n последним идет умножение A1..s[1,n] на As[1,n]+1..n. Предшествующие умножения можно найти рекурсивно: значение s[1,s[1,n]] определяет последнее умножение при нахождении A1..s[1,n], a s[s[l,n]+1,n] определяет последнее умножение при вычислении As[1,n]+1..n. Рекурсивная процедура вычисляет произведение Ai..j и расставляет скобки в этом произведении, имея следующие данные: последовательность матриц {A1, A2, ..., An} , таблицу s, найденную процедурой MATRIX_CHAIN_ORDER, а также индексы i и j. Текст этой процедуры можно посмотреть здесь.
На выходе из процедуры получаем произведение матриц A и расстановку скобок R. Причем R – это массив строк, каждый элемент соответствует матрице. Расставлять скобки начинаем с последнего произведения, и записываем этот результат в две ячейки R[s[i, j]] и R[j], так как перемножаем две матрицы. Далее идет перемножение следующих матриц, определяемых s[i, j] и j. Сначала производими сравнивнения R[s[i, j]] <> '' и R[j] <> '', и, в зависимости от полученного результата, записываем следующее перемножение (так же в две ячейки). Рекурсия происходит пока i > j, иначе C присваиваем i-ю матрицу U, а в R[i,j] ничего не заносим. Процедура MATRIX_MULTIPLY(C, X, Y, p[s[i, j]],p[j],p[i-1],p[s[i, j]]) перемножает матрицы X*Y и результат помещает в матрицу С. p[s[i, j]], p[j], p[i-1], p[s[i, j]] – разрядность матриц X, Y, а P – массив из разрядностей. В конце процедуры матрице A присваиваем значение матрицы C.
В основной части программы при этом должно находиться обращение к процедурам MATRIX_CHAIN_ORDER и MATRIX_CHAIN_MULTIPLY. Перед обращением к этим процедурам необходимо задать число матриц и сами матрицы.
Решение вы можете посмотреть
здесь.
(1)Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2000.-960с.,263 ил.
На следующем шаге мы разберем решение задачи "Головоломка умножения".
