Здесь мы разберем решение задачи "Чебурашка".
В таблице размером N*N, где N<13, клетки заполнены случайным образом цифрами от 0 до 9. Предложить Чебурашке алгоритм, позволяющий найти маршрут из клетки (1, 1) в клетку (N, N) и удовлетворяющий следующим условиям:
- любые две последовательные клетки в маршруте имеют общую сторону;
- количество клеток маршрута минимально;
- сумма цифр в клетках маршрута максимальна. [1].
Будем искать наилучшие пути, идущие из клетки A[1,1] во все остальные клетки таблицы, в частности и в клетку A[N,N]. Для этого в некоторой вспомогательной таблице B того же размера, что и A, будем отмечать суммы цифр оптимальных путей, ведущих в соответствующие клетки. Так в клетке B[1,1] окажется число A[1,1], так как путь, ведущий в нее, состоит из одной клетки. Так же легко заполняются клетки B[1,2] и B[2,1]. В них тоже ведут единственные пути и суммы цифр вдоль них равны A[1,1]+A[1,2] и A[1,1]+A[2,1] соответственно.
Поясним сказанное на конкретном примере. Пусть таблица A размером 5*5 имеет вид, представленный на рисунке 1. Нумерация клеток идет от левого верхнего угла. Проследим за заполнением таблицы B. О клетках B[1,2] и B[2,1] уже говорилось. В клетку B[2,2] можно попасть либо из клетки B[1,2], либо из клетки B[2,1]. Следовательно, в клетку B[2,2] надо записать либо число B[1,2] + A[2,2], либо число B[2,1] + A[2,2], в зависимости от того, какое из них больше. Заполнение остальных клеток таблицы B аналогично. Заполнение матрицы B показано на рисунке 2.
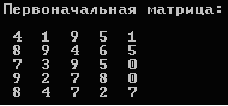
Рис.1. Первоначальная матрица A
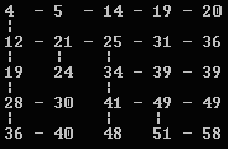
Рис.2. Матрица B
Если путь, ведущий в эту клетку один, то в клетку вписывается сумма цифр вдоль этого пути. Такими клетками являются клетки вида B[1,j] и B[j,1].
Если же в клетку B[i,j] можно попасть из клеток, для которых подсчитаны значения B, то необходимо выбрать максимальное из B[i,j-1] и B[i-1,j] и записать в клетку B[i,j] максимальное число плюс A[i,j].
Клетку B[i,j] соединим чертой с той клеткой, где был достигнут максимум. Для нахождения искомого маршрута достаточно пройти из клетки (N,N) в клетку (1,1) по черточкам.
Входными данными в этой задачи является размерность матрицы n. При вводе n проверятся удовлетворяет ли введенное число условию задачи: 0 < N < 13. Двумерный массив A - это первоначальная матрица. Она заполняется псевдослучайными числами. Двумерный массив B – это описанная выше матрица суммы цифр оптимальных путей, ведущих в соответствующие клетки. Процедура vivod(A) используется для вывода на экран соответствующей матрицы. Матрица U используется для нахождения пути следования в двумерном массиве B. В ячейках матрице U может содержаться либо 0, если в клетку b[i, j] попали сверху b[i-1, j], либо 1, если попали слева b[i, j-1]. Так как в первой строке и в первом столбце можем двигаться только в одном направлении, то организован цикл, заполняющий матрицы U и B соответствующими значениями. Далее идет заполнение оставшихся ячеек матриц U и B. Функция max(B[i-1,j],B[i,j-1],p) ищет максимальное значение среди B[i-1,j] и B[i,j-1], и присваивает p единицу, если второе значение больше первого, иначе p остается равным 0. B[i, j] получает значение, равное сумме A[i, j] и максимального из B[i-1,j] и B[i,j-1]. Значению U[i, j] присваивается значение p. Таким образом, заполняются таблицы U и B. Процедура vivodB(B) выводит на экран значения двумерного массива B. При этом показано, каким образом получена эта матрица (благодаря матрице U). То есть выводится рисунок 2. В матрице C хранятся координаты искомого маршрута (строка, столбец). Так как требуется найти минимальный путь, а минимальное количество равно 2N-1, где N размерность матрицы, то количество строк в матрице C будет равно 2N-1. Первая клетка маршрута это (1,1), последняя (n,n). Заполнение матрицы C начинаем с последней клетки. В зависимости от того, какое из соседних чисел в матрице B максимальное (сверху или слева) уменьшаем значение строки или столбца. И записываем координаты этих ячеек в матрицу C. После заполнения матрицы C «обнуляем» матрицу U, для показа пути следования в матрице A. Затем заполняем матрицу U, используем при этом матрицу C. Учитываем при этом, какие строки и столбцы координат изменились. Далее выводим на экран матрицу A с путем следования в ней (процедура vivodB(A)). На рисунке 3 показана матрица A с путем следования из клетки (1,1) в (n,n). Далее выводим координаты маршрута следования в матрице A, то есть выводим матрицу C (рис. 4).
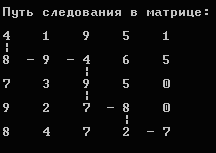
Рис.3.Матрица A и путь следования в ней

Рис.4. Координаты маршрута следования в матрице A
Решение вы можете посмотреть
здесь.
(1)Статья "Динамическое программирование и жадные алгоритмы" (http://kitnet.altnet.ru/www/metod/ book3/doc1/str1.htm)
На следующем шаге мы разберем решение задачи "Маршрут".
