На этом шаге мы рассмотрим свойства энтропии.
- Как следует из (1.4), H = 0 только в двух случаях:
- какая-либо из p(Aj) = 1; однако, при этом следует, что все
остальные p(Ai) = 0 (i
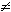 j), т.е.
реализуется ситуация, когда один из исходов является достоверным (и общий итог
опыта перестает быть случайным);
j), т.е.
реализуется ситуация, когда один из исходов является достоверным (и общий итог
опыта перестает быть случайным);
- все p(Ai) = 0, т.е. никакие из
рассматриваемых исходов опыта невозможны, поскольку нетрудно показать, что:
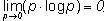
Во всех остальных случаях, очевидно, что H > 0.
- какая-либо из p(Aj) = 1; однако, при этом следует, что все
остальные p(Ai) = 0 (i
- Очевидным следствием (1.1) будет утверждение,
что для двух независимых опытов
 и
и
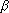
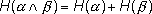 (1.5)
(1.5)
- Энтропия сложного опыта, состоящего из нескольких независимых, равна сумме энтропий отдельных опытов.
В справедливости (1.5) можно убедиться непосредственно.
Пусть опыт ![]() имеет n
исходов A1, A2, ..., An, которые реализуются с
вероятностями p(A1), p(A2), ..., p(An), а событие
имеет n
исходов A1, A2, ..., An, которые реализуются с
вероятностями p(A1), p(A2), ..., p(An), а событие
![]() – m
исходов B1, B2, ..., Bm с вероятностями
p(B1), p(B2), ..., p(Bm). Сложный опыт
– m
исходов B1, B2, ..., Bm с вероятностями
p(B1), p(B2), ..., p(Bm). Сложный опыт
![]() имеет n ·m исходов типа AiBj
(i=1...n, j=1...m). Следовательно:
имеет n ·m исходов типа AiBj
(i=1...n, j=1...m). Следовательно:
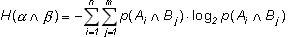 (1.6)
(1.6)
Поскольку ![]() и
и
![]() –
независимы, то независимыми окажутся события в любой паре
Ai
–
независимы, то независимыми окажутся события в любой паре
Ai![]() Bj.
Тогда:
Bj.
Тогда:
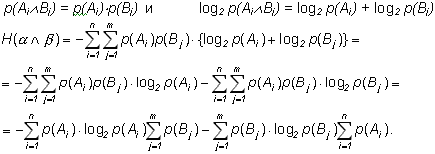
В слагаемых произведено изменение порядка суммирования в соответствии со значениями индексов. Далее, по условию нормировки:

а из (1.4)
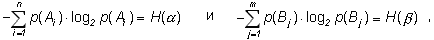
Окончательно имеем:
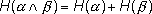
что и требовалось доказать.
Пусть имеется два опыта с одинаковым числом исходов n, но в одном случае они равновероятны, а в другом – нет. Каково соотношение энтропий опытов? Примем без доказательства следующее утверждение:
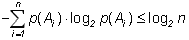 (1.7)
(1.7)
При прочих равных условиях наибольшую энтропию имеет опыт с равновероятными исходами.
Другими словами, энтропия максимальна в опытах, где все исходы равновероятны. Здесь усматривается аналогия (имеющая глубинную первооснову!) с понятием энтропии, используемой в физике. Впервые понятие энтропии было введено в 1865 г. немецким физиком Рудольфом Клаузиусом как функции состояния термодинамической системы, определяющей направленность самопроизвольных процессов в системе. Клаузиус сформулировал II начало термодинамики. В частности, он показал, что энтропия достигает максимума в состоянии равновесия системы. Позднее (в 1872 г.) Людвиг Больцман, развивая статистическую теорию, связал энтропию системы с вероятностью ее состояния, дал статистическое (вероятностное) толкование II-му началу термодинамики и, в частности, показал, что вероятность максимальна у полностью разупорядоченной (равновесной) системы, причем, энтропия и термодинамическая вероятность оказались связанными логарифмической зависимостью. Другими словами, в физике энтропия оказывается мерой беспорядка в системе. При этом беспорядок понимается как отсутствие знания о характеристиках объекта (например, координат и скорости молекулы); с ростом энтропии уменьшается порядок в системе, т.е. наши знания о ней. Сходство понятий и соотношений между ними в теории информации и статистической термодинамике, как оказалось позднее, совершенно не случайно.
Кстати, результат, полученный в рассмотренном на предыдущем шаге примере, иллюстрирует справедливость формулы (1.7).
На следующем шаге мы рассмотрим понятие условной энтропии.
