На этом шаге мы рассмотрим перевод дробных чисел из одной системы счисления в другую.

Вещественное число, в общем случае содержащее целую и дробную часть, всегда можно представить в виде суммы целого числа и правильной дроби. Поскольку в предыдущем шаге проблема записи натуральных чисел в различных системах счисления уже была решена, можно ограничить рассмотрение только алгоритмами перевода правильных дробей. Введем следующие обозначения: правильную дробь в исходной системе счисления p будем записывать в виде 0,Y_p, дробь в системе q – 0,Y_q, а преобразование – в виде 0,Y_p 0,Y_q. Последовательность рассуждений весьма напоминает проведенную ранее для натуральных чисел. В частности, это касается рекомендации осуществлять преобразование через промежуточный переход к 10-й системе, чтобы избежать необходимости производить вычисления в "непривычных" системах счисления, т.е. 0,Y_p0,Y₁₀ 0,Y_q. Это, в свою очередь, разбивает задачу на две составляющие: преобразование 0,Y_p 0,Y₁₀ и 0,Y₁₀0,Y_q, каждое из которых может рассматриваться независимо.

Алгоритмы перевода 0,Y₁₀ 0,Y_q выводится путем следующих рассуждений. Если основание системы счисления q, простая дробь содержит n цифр и b_k – цифры дроби (1k n, 0 b_k q–1), то она может быть представлена в виде суммы:

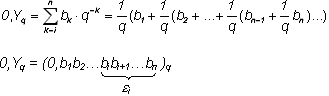(5)

Часть дроби от разряда i до ее конца обозначим _i и примем _n = b_n/q (очевидно, ₁ = 0,Y_q); тогда в (5) легко усматривается рекуррентное соотношение:

(6)

Если вновь позаимствовать в PASCAL’е обозначение функции – на этот раз trunc, которая производит округление целого вещественного числа путем отбрасывания его дробной части, то следствием (6) будут соотношения, позволяющие находить цифры новой дроби:

b_i = trunc(q·_i),

_i+1 = q·_i - trunc(q·_i) (7)

Соотношения (7) задают алгоритм преобразования 0,Y₁₀ 0,Y_q:

умножить исходную дробь в 10-й системе счисления на q, выделить целую часть – она будет первой цифрой новой дроби; отбросить целую часть;
для оставшейся дробной части операцию умножения с выделением целой и дробных частей повторять, пока в дробной части не окажется 0 или не будет достигнута желаемая точность конечного числа (exact); появляющиеся при этом целые будут цифрами новой дроби;
записать дробь в виде последовательности цифр после нуля с разделителем в порядке их появления в п (1) и (2).

Блок-схема алгоритма представлена на рисунке 1. Цикл перевода заканчивается либо в том случае, когда окажется _i+1 = 0, либо последовательность действий повторится наперед заданное число раз (значение константы ex), которое совпадает с количеством значащих цифр в дробной части.

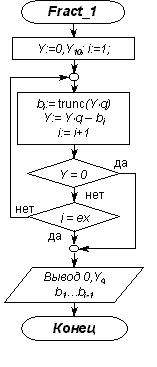
Рис.1. Блок-схема алгоритма

Пример 4. Выполнить преобразование 0,375₁₀

0,Y2.

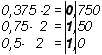
Таким образом, 0,375₁₀ = 0,011₂.

Перевод 0,Yp0,Y10, как и в случае натуральных чисел, сводится к вычислению значения формы (5) в десятичной системе счисления. Например,

0,011₂ = 0·2^-1 + 1·2^-2 + 1·2^-3 = 0,25 + 0,125 = 0,375₁₀

Следует сознавать, что после перевода дроби, которая была конечной в исходной системе счисления, она может оказаться бесконечной в новой системе. Соответственно, рациональное число в исходной системе может после перехода превратиться в иррациональное. Справедливо и обратное утверждение: число иррациональное в исходной системе счисления в иной системе может оказаться рациональным.

Пример 5. Выполнить преобразование 5,3(3)₁₀

Перевод целой части, очевидно, дает: 5₁₀ = 12₃. Перевод дробной части: 0,3(3)₁₀ = 0,1₃. Окончательно: 5,3(3)₁₀ = 12,1₃.

Как уже было сказано, значение целого числа не зависит от формы его представления и выражает количество входящих в него единиц. Простая дробь имеет смысл доли единицы, и это "дольное" содержание также не зависит от выбора способа представления. Другими словами, треть пирога остается третью в любой системе счисления.

На следующем шаге мы рассмотрим понятие экономичности системы счисления.

Предыдущий шаг Содержание Следующий шаг