На этом шаге мы рассмотрим однородный двоичный симметричный канал.
Пусть на вход канала подаются сигналы двух типов (a1 и a2 – например, импульс и пауза) и они же принимаются на выходе, т.е. {a} = {b}, m = n. Пусть, далее, вероятность ошибки передачи для обоих сигналов одинакова и равна p; тогда, для дополнительных событий вероятность безошибочной передачи равна 1 - p. Применяя принятые выше обозначения, можно записать:
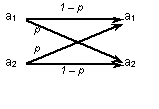
Рис.1. Представление канала в виде графа
Такой канал называется двоичным симметричным (относительно инверсии
a1
a2);
схематически его можно представить в виде графа (см. рис. 1).
Линии со стрелками указывают, в какие принимаемые сигналы могут перейти те, что
отправлены на входе; рядом со стрелками указаны вероятности соответствующих
переходов.
Найдем пропускную способность канала, воспользовавшись определением (7). Оно, в свою очередь, требует вычисления I(b,a) (или I(a,b)) и установления ее максимума как функции p. Если по-прежнему опыт a состоит в распознавании сигнала на входе канала, а опыт b – на выходе, с учетом того, что b1 = a1, а b2 = a2, и воспользовавшись выражением (6), получаем:
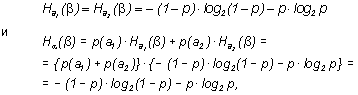
поскольку p(a1) + p(a2)= 1 как достоверное событие. Другими словами, в рассматриваемом канале энтропия Ha(b) не зависит от значений p(a1) и p(a2), а определяется только вероятностью искажений сигнала при передаче. Следовательно,
C = L · max{H(b) + (1 – p) + p · log2p}
Поскольку m = 2, max{H(b)} = 1. Таким образом, окончательно для пропускной способности симметричного двоичного канала имеем:
C = L {1 + (1 – p) · log2(1 – p) + p log2p}
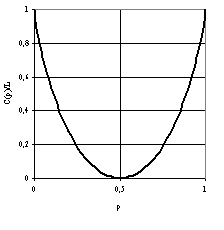
Рис.2. График функции C(p)
График функции C(p) изображен на рис. 2. Максимального значения равного L функция C(p) достигает при p = 0 (очевидно, это означает отсутствие помех) и при p = 1 – это соответствует ситуации, когда канал полностью инвертирует входные сигналы (т.е. заменяет 0 на 1, а 1 на 0) - это не служит препятствием для однозначной идентификации посланного сигнала по принятому и, следовательно, не снижает пропускной способности канала. Во всех остальных ситуациях 0 < p < 1 и C(p) < L. Наконец, при p = 0,5 пропускная способность становится равной 0 – это вполне естественно, поскольку вероятность искажения 0,5 означает, что независимо от того, какой сигнал был послан, на приемном конце с равной вероятностью может появиться любой из двух допустимых сигналов. Ясно, что передача в таких условиях оказывается невозможной.
Поскольку канал двоичный, согласно (3) L = C0. Произведя соответствующую замену, получим:
C = C0 {1 + (1 – p) log2(1 – p) + p log2p} (8)
В выражение в
фигурных скобках не превышает 1, следовательно, справедливо соотношение:
С 
C0,
т.е. можно считать доказанным, что наличие помех снижает пропускную способность
(и даже может сделать ее равной 0).
Пример 3. Каково отношение C/C0, если средняя частота появления ошибки при передаче сообщения в двоичном симметричном канале составляет 1 ошибочный сигнал на 100 переданных?
Очевидно, вероятность появления ошибки передачи p = 0,01. Следовательно, из (8) получаем:
т.е. пропускная способность канала снизилась приблизительно на 8%.
Следует заметить, что отношение C/C0 убывает при увеличении вероятности искажения довольно быстро, что иллюстрируется таблицей:
| Число ошибок передачи (на 100) | 1 | 10 | 25 | 50 |
|---|---|---|---|---|
| Вероятность ошибки | 0,01 | 0,10 | 0,25 | 0,50 |
| С/С0 | 0,92 | 0,53 | 0,19 | 0 |
На следующем шаге мы рассмотрим однородный симметричный канал со стиранием.
