На этом шаге мы дадим общую характеристику машине Тьюринга.
Машина Тьюринга подобна машине Поста, но функционирует несколько иначе. Машина Тьюринга (МТ) состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0, q1, ..., qs, принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний). При этом q0 называется начальным состоянием.
Читающая и пишущая головка может читать буквы рабочего алфавита А = {a0, а1, ...,аt}, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква a0 - «пробел». Головка находится в каждый момент времени над некоторой ячейкой ленты - текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты. При этом возможна ситуация выхода за левый край ленты (ЛК), которая является аварийной (недопустимой), или машинного останова (МО), когда машина выполняет предписание об остановке.
Порядок работы МТ (с рабочим алфавитом a0, а1 ..., аt и состояниями q0, q1, ..., qs) описывается таблицей машины Тьюринга. Эта таблица является матрицей с четырьмя столбцами и (s + 1)(t + 1) строками. Каждая строка имеет вид
qi aj vij qij, 0 <= i < s, 0 <= j <= t, где qij принадлежит {q0,q1,…, qs}
Здесь через vij обозначен элемент объединения алфавита {a0, а1, ..., аt} и множества предписаний для лентопротяжного механизма:
- l - переместить ленту влево,
- r - переместить ленту вправо,
- s - остановить машину;
- vij - действие МТ, состоящее либо в занесении в ячейку ленты символа алфавита a0, а1, ..., аt либо в движении головки, либо в останове машины;
- qij является последующим состоянием.
МТ работает согласно следующим правилам: если МТ находится в состоянии qi, головка прочитывает символ aj в рабочей ячейке. Пусть строка ai aj vij qij, начинающаяся с символов qiaj, встречается только один раз в таблице. Если vij - буква рабочего алфавита, то головка стирает содержимое рабочей ячейки и заносит туда эту букву. Если vij – команда r или l для лентопротяжного механизма, то лента сдвигается на одну ячейку вправо или влево (если не происходит выход за край ленты) соответственно. Если vij = s, то происходит машинный останов.
Машина Тьюринга начинает работу из некоторой начальной конфигурации, включающей в себя начальное состояние (обычно q0) и положение считывающе-записывающей головки над определенной ячейкой ленты, содержащей один из символов рабочего алфавита А.
Отметим, что наличие разнообразных символов в рабочем алфавите МТ позволяет представлять на ленте произвольную текстовую и числовую информацию, а переходы управляющего центра МТ в различные состояния моделируют запоминание машиной Тьюринга промежуточных результатов работы. Таблица, определяющая порядок работы МТ, не является в прямом смысле слова программой (ее предписания выполняются не последовательно, одно за другим, а описывают преобразования символов некоторого текста, находящегося на ленте). Таблицу МТ часто называют схемой машины Тьюринга или попросту отождествляют с самой машиной Тьюринга, коль скоро ее устройство и принцип функционирования известны.
Рассмотрим примеры нескольких схем машины Тьюринга.
1. Алгоритм прибавления единицы к числу в десятичной системе счисления.
Дана десятичная запись числа n (т.е. представление натурального числа n в десятичной системе счисления). Требуется получить десятичную запись числа n+1.
Очевидно, что внешний алфавит МТ должен состоять из десяти цифр 1 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и символа пробела _. Эти цифры записывают по одной в ячейке (подряд, без пропусков).
Оказывается достаточным иметь два внутренних состояния машины: q1 и q2.
Предположим, что в начальный момент головка находится над одной из цифр j числа, а машина находится в состоянии q1. Тогда задача может быть решена в два этапа: движения головки к цифре единиц числа (во внутреннем состоянии q1) и замене этой цифры на единицу большую (с учетом переноса 1 в следующий разряд, если это 9, j во внутреннем состоянии q2). Соответствующая схема МТ может иметь вид
| ai | qi | |
|---|---|---|
| q1 | q2 | |
| 0 | 0 П q1 | 1 C q2 |
| 1 | 1 П q1 | 2 C q2 |
| 2 | 2 П q1 | 3 C q2 |
| 3 | 3 П q1 | 4 C q2 |
| 4 | 4 П q1 | 5 C q2 |
| 5 | 5 П q1 | 6 C q2 |
| 6 | 6 П q1 | 7 C q2 |
| 7 | 7 П q1 | 8 C q2 |
| 8 | 8 П q1 | 9 C q2 |
| 9 | 9 П q1 | 0 C q2 |
| _ | _ Л q1 | 1 C q2 |
2. Алгоритм записи числа в десятичной системе счисления.
Дана конечная последовательность меток, записанных в клетки ленты подряд, без пропусков. Требуется записать в десятичной системе число этих меток (пересчитать метки).
Суть алгоритма может состоять в том, что к числу 0, записанному на ленте в начале работы машины, машина добавляет 1, стирая метку за меткой, так что вместо нуля возникает число 0+k.
Легко могут быть построены алгоритмы сложения чисел, их перемножения, нахождения наибольшего общего делителя и т.д. Однако главная цепь введения машин Поста и Тьюринга не программирование для них, а изучение свойств алгоритмов и проблемы алгоритмической разрешимости задач.
В зависимости от числа используемых лент, их назначения и числа состояний устройства управления можно рассматривать различные модификации машин Тьюринга.
Предположим, мы расширили определение МТ, добавив определенное состояние q* устройства управления машины. Будем говорить, что если устройство управления переходит в состояние q0 для заданного входного слова x, то машина допускает x; если устройство переходит в состояние q*, то машина запрещает x. Такую машину будем называть машиной Тьюринга с двумя выходами. Могут быть рассмотрены многочисленные варианты машины Тьюринга, имеющие некоторое конечное число лент. В каждой клетке этих лент может находиться один из символов внешнего алфавита А = {а0, а1, ..., аn}. Устройство управления машиной в каждый момент времени находится в одном из конечного множества состояний Q = {q0, q1, ..., qm). Для k-ленточной машины конфигурация ее в i-й момент времени описывается системой k-слов вида:
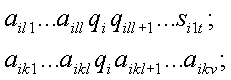
первый индекс соответствует моменту времени, второй – номеру ленты, третий – номеру клетки, считая слева направо. Говорят, что машина выполняет команду
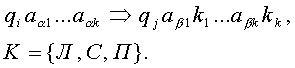
Если, находясь в состоянии q1, и обозревая ячейки с символами аa1, ..., aak, машина переходит в состояние qj, заменяя содержимое ячеек соответственно символами аb1, ..., abk, то после этого ленты соответственно сдвигаются в направлениях k1, ..., kk.
До сих пор принималось, что различные алгоритмы осуществляются на различных машинах Тьюринга, отличающихся набором команд, внутренним и внешним алфавитами. Однако можно построить универсальную машину Тьюринга, способную выполнять любой алгоритм любой машины Тьюринга. Это достигается путем кодирования конфигурации и программы любой данной машины Тьюринга в символах внешнего алфавита универсальной машины. Само кодирование должно выполняться следующим образом:
- различные символы должны заменяться различными кодовыми группами, но один и тот же символ должен заменяться всюду, где бы он не встретился, одной и той же кодовой группой;
- строки кодовых записей должны однозначно разбиваться на отдельные кодовые группы;
- должна иметься возможность распознать кодовые группы, соответствующие командам Л, П, С, различать кодовые группы, соответствующие символам внешнего алфавита и внутренним состояниям.
Для сравнения структур различных машин и оценки их сложности необходимо иметь соответствующую меру сложности машин. К.Шеннон предложил рассматривать в качестве такой меры произведение числа символов внешнего алфавита и числа внутренних состояний. Большой интерес вызывает задача построения универсальной машины Тьюринга наименьшей сложности.
Может быть рассмотрено еще одно обобщение машин Тьюринга: их композиции. Операции композиции, выполняемые над алгоритмами, позволяют образовывать новые, более сложные алгоритмы из ранее известных простых алгоритмов. Поскольку машина Тьюринга - алгоритм, то операции композиции применимы и к машинам Тьюринга. Рассмотрим основные из них: произведение, возведение в степень, итерацию.
Пусть заданы машины Тьюринга T1 и Т2, имеющие общий внешний алфавит A = {a0, a1, …, аm} и внутренние состояния Q1 = {q0, q1, ..., qn} и Q2 = {q0, g1, ..., qt} соответственно. Композицией или произведением машины T1 и машины Т2 будем называть машину Т с тем же внешним алфавитом A = {a0, a1, …, аm} и набором внутренних состояний Q = {q0, q1, …,qn, qn+1, …, qn+t} и программой, эквивалентной последовательному выполнению программ машин Т1 и Т2:
T = T1 * Т2
Таким же образом определяется операция возведения в степень: n-й степенью машины T называется произведение T ... Т с n сомножителями.
Операция итерации применима к одной машине и определяется следующим образом. Пусть машина Т1 имеет несколько заключительных состояний. Выберем ее r-е заключительное состояние и отождествим его в схеме машины с ее начальным состоянием. Полученная машина является результатом итерации машины Т1: T = Т1.
На следующем шаге мы рассмотрим нормальные алгоритмы Маркова.
