На этом шаге мы рассмотрим основные свойства операции подстановки.
- Свойство 1.
- Операция подстановки сохраняет свойство всюду определенности функций, т.е. если функция g(y1, ...,ym) и функции h1(x1, ...,xn), h2(x1, ...,xn), ..., hm(x1, ...,xn) всюду определенные функции и функция f получается из них с помощью операции подстановки, то f также является всюду определенной функции.
- Доказательство.
- Пусть h1, h2, ..., hm произвольные функции от n переменных. Рассмотрим произвольный набор
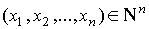. Тогда h1, h2, ..., hm будут определены в этом наборе в силу свойства всюду определенности. Функция g
будет определена на наборе (h1(x1, ...,xn), h2(x1, ...,xn), ..., hm(x1, ...,xn))
в силу свойства всюду определенности, а по определению подстановки это и есть функция f.
Таким образом, мы доказали, что функция f определена на наборе (x1, ...,xn). Так как мы взяли произвольный набор из множества натуральных чисел, то свойство доказано.
- Свойство 2.
- Операция подстановки сохраняет свойство алгоритмической вычислимости функций, т.е. если функции g(y1, ...,ym) и h1, h2, ..., hm алгоритмически вычислимы, и f = S(q, h1, h2, ..., hm), то существует алгоритм Af, вычисляющий функцию f.
- Доказательство.
- Пусть задан произвольный набор
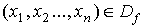. Это означает, что этот набор
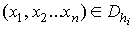, где i=1, 2, ..., m. Далее поступаем следующим образом:
- 1-й шаг: применяем к набору (x1, ...,xn) алгоритм A1, вычисляющий функцию h1. Так как функция h1 по условию алгоритмически вычислимая функция, то за конечное число шагов алгоритм A1 дает конечный результат для функции h1.
- 2-й шаг: применяем к набору (x1, ...,xn) алгоритм A2, вычисляющий функцию h2. Так как функция h2 по условию алгоритмически вычислимая функция, то через конечное число шагов работа алгоритма Ф2 завершается результативно, т.е. будут вычислено значение функции h2 на наборе (x1, ...,xn) и т.д. Если работа всех алгоритмов A1, A2, ..., Am на наборе (x1, ...,xn) завершилась результативно, т.е. вычислены соответствующие значения (h1(x1, ...,xn), h2(x1, ...,xn), ..., hm(x1, ...,xn)), то переходим на следующий шаг, т.е.
- m+1-й шаг: применяем алгоритм Ag, вычисляющий функцию g, к набору (h1(x1, ...,xn), h2(x1, ...,xn), ..., hm(x1, ...,xn)). В силу свойства алгоритмически вычислимости функции g, через конечное число шагов алгоритм Ag завершает работу на наборе (h1(x1, ...,xn), h2(x1, ...,xn), ..., hm(x1, ...,xn)) результативно, и этот результат будем считать значением функции f, так как по определению операции подстановки f(x1, ...,xn) = g(h1(x1, ...,xn), h2(x1, ...,xn), ..., hm(x1, ...,xn)).
В случае, когда алгоритм Ai, где i=1, 2, ..., m не останавливается или завершает работу нерезультативно, будем считать, что искомый алгоритм для вычисления данной функции, т.е. функции f(x1, ...,xn), не существует.
Операция примитивной рекурсии
Пусть задана функция g(x1, ...,xn) и функция h(x1, ..., xn, y, z).
Определение. Говорят, что функция f(x1, ..., xn, y) получена из функций g(x1, ...,xn) и h(x1, ..., xn, y, z) с помощью операции примитивной рекурсии, если выполняются следующие равенства:
f(x1, ..., xn, 0) = g(x1, ..., xn)
f(x1, ..., xn, y+1) = h(x1, ..., xn, y, f(x1, ..., xn,y))
Это определение имеет смысл, когда n<>0, при этом записывается
f(x1, ..., xn, y) = R(g(x1, ..., xn), h(x1, ..., xn, y, z))
или сокращенно f = R(g,h), где R означает операции примитивной рекурсии.
В случае, когда n=0, то операция примитивной рекурсии примет вид:
и обозначается:
На следующем шаге мы рассмотрим основные свойства операции примитивной рекурсии.
