На этом шаге мы рассмотрим кусочное задание функции.
Пусть задана совокупность функций {f1, ..., fk, fk+1} и совокупность предикатов {p1, ..., pk}, где fi = fi(x1,..., xn), i=1, 2, ..., k, k+1 и pj = pj(x1,..., xn), j=1, 2, ..., k, причем области истинности предикатов попарно не пересекаются.
Введем следующие обозначения: x = (x1,..., xn).
Определение. Говорят, что функция f(x) задана кусочным образом относительно заданной совокупности функций и предикатов, если она удовлетворяет следующим условиям:
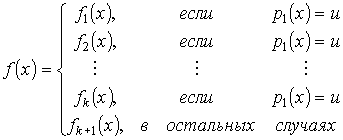(31)
- Теорема 4.
- Функция f(x), заданная кусочным образом из совокупности {f1, ..., fk, fk+1, p1, ..., pk} = Ψ, является ПРФ относительно Ψ.
- Доказательство.
- Пусть φi(x) - представляющая функция для предиката pi(x), где 1<=i<=k.
Тогда покажем, что функцию f(x) можно представить следующим образом:
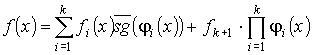(32)
1) Рассмотрим произвольный набор
.
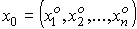Пусть для какого - то i0 pi0(x0) = и, где 1<=i0<=k. Тогда по определению представляющей функции предиката, получаем, что φpi0(x0) = 0, следовательно
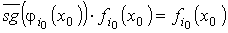
а для всех остальных i <> i0 , pi(x0)=л, отсюда
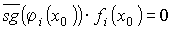
Таким образом, в данном случае, мы получаем, что:
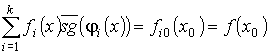
2) Предположим, что для любого i pi(x0) = л, тогда φi(x0) = φk(x) = 1, где 1<=i<=k. Следовательно,
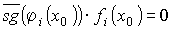, а
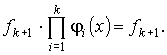
Из пунктов 1-2 следует, что на множестве Nn функция
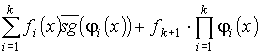
совпадает с функцией f(x), которая задана кусочным образом из совокупности Ψ. Так как операции конечного суммирования и конечного произведения сохраняют свойством примитивной рекурсивности функций, следовательно, рассматриваемая функция является ПРФ относительно Ψ. Что требовалось доказать.
Пример. Предположим, что задана примитивно рекурсивная функция f(x1, ..., xn).
Рассмотрим конечное число точек, произвольным образом поменяем значения функции в каждой точке x1, ..., xk и полученную функцию обозначим через f1(x), т.е.
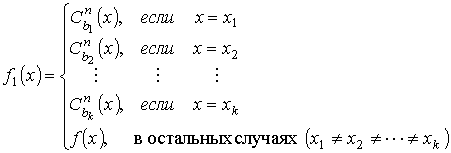
Возникает вопрос: сохраняет ли функция f(x1, ..., xn) свойство примитивной рекурсивности?
Как видим, функция f1(x) - примитивно рекурсивная функция как заданная кусочным образом из совокупности примитивно рекурсивных функций и предикатов.
В качестве функций fj, j = 1, 2, ..., k взяты элементарные функции
и в качестве предиката взят предикат равенства, т.е.
pj(x) = (xj = x), j = 1, 2, ..., k. Так как точки xj по условию задачи отличаются друг от друга,
то области истинности предикатов pj попарно не пересекаются.
Таким образом, функция f(x1, ..., xn) сохраняет свойство примитивной рекурсивности.
- Лемма 1.
- Подстановка примитивно рекурсивной функции в предикат равенства есть примитивно рекурсивный предикат.
- Доказательство.
- Пусть заданы примитивно рекурсивные функции φ1(x), φ2(y)
и пусть p(x,y) = (x=y) - предикат равенства.
Рассмотрим предикат вида p(φ(x),φ(y)) = (φ(x)=φ(y)). Он является примитивно рекурсивным предикатом. Действительно, для данного предиката представляющей функцией является функция вида φp =
Sg(|φ1(x)-φ2(y)|) , которая является ПРФ.
На следующем шаге мы рассмотрим операцию ограниченной минимизации.
