На этом шаге мы рассмотрим верхние и средние оценки сложности алгоритма.
Для приведенного на предыдущем шаге алгоритма вычисления факториала вычислили точную оценку сложности. Для многих других алгоритмов также может быть (с большими или меньшими усилиями) найдена точная оценка. Такими алгоритмами являются известные алгоритмы решения систем линейных уравнений методом Гаусса, перемножения матриц, вычисления значений многочленов. Для них просто отыскать параметр V сложности исходных данных - это размер матрицы или степень многочлена. Сложность алгоритма при этом однозначно зависит от V.
Многие же задачи характеризуются большим количеством исходных данных. Вводя интегральный параметр V объема (сложности) данных, неявно предположено, что все множество комбинаций значений исходных данных может быть разбито на классы. В один класс попадают комбинации с одним и тем же значением V. Для любой комбинации из заданного класса алгоритм будет иметь одинаковую сложность (исполнитель выполнит одно и то же количество операций). Иначе говоря, функция c = сложность_α(X) может быть разложена в композицию функций V= r(Х) и c = Тα(V), где r - преобразование значений x1, x2, x3, ...,xn в значение V.
Действительно, для рассмотренных примеров вычисления факториала и скалярного произведения это было так. Но нет никаких причин надеяться, что это будет выполняться для любых алгоритмов, учитывая наше желание представлять функции формулами с использованием общеизвестных элементарных функций (или, как говорят, в аналитическом виде).
Выход состоит в следующем. Множество D комбинаций исходных данных все-таки разбивается "каким-либо разумным образом" на классы, и каждому классу приписывается некоторое значение переменной V. Например, если мы хотим оценить сложность алгоритма анализа арифметических выражений, то в один класс можно поместить все выражения, состоящие из одинакового числа символов (строки одинаковой длины) и переменную V сделать равной длине строки. Это разумное предположение, так как с увеличением длины сложность должна увеличиваться: припишем к выражению длины n строку +1 - получится выражение длины n+2, требующее для анализа больше операций, чем предыдущее. Но строгого (линейного) порядка нет. Среди выражений длины n может найтись более сложное (в смысле анализа), чем некоторое выражение длины n+2, не говоря уже о том, что среди выражений равной длины будут выражения разной сложности.
Затем для каждого класса (с данным значением V) оценивается количество необходимых операций в худшем случае, т.е. для набора исходных данных, требующих максимального количества операций обработки (сложность для худшего случая - верхняя оценка), и в лучшем случае - для набора, требующего минимального количества операций. Таким образом, получаются верхняя и нижняя оценки сложности алгоритма (рисунок 1).
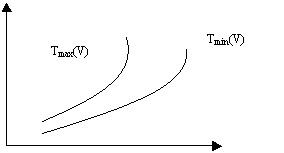
Рис.1. Зависимость сложности алгоритма от сложности данных
Разница между Tmax(V) и Tmin(V) может быть значительной. Но для многих алгоритмов отмечается ситуация "редкости крайних значений": только на относительно небольшом количестве сочетаний исходных данных реализуются близкие к верхним или нижним оценкам значения сложности. Поэтому интересно бывает отыскать некоторое "усредненное" по всем данным число операций (средняя оценка). Для этого привлекаются комбинаторные методы или методы теории вероятностей. Полученное значение и считается значением Тα(V) средней оценки.
Функции сложности для худшего случая и для средних оценок имеют практическое значение. Системы реального времени, работающие в очень критических условиях, требуют, чтобы неравенство Тα(X)<Tmах не нарушалось никогда; в этом случае нам нужна оценка для худшего случая. В других системах достаточно, чтобы это неравенство выполнялось в большинстве случаев; тогда мы используем среднюю оценку. Опять же в связи со свойством массовости алгоритма исследователей чаще интересуют именно средние оценки, но получать их обычно труднее, чем верхние оценки.
На следующем шаге мы рассмотрим основные методы и приемы анализа сложности.
