На этом шаге мы рассмотрим число вырожденных деревьев.

    Вырожденное дерево - это линейный список. Мы уже приводили примеры вырожденных деревьев: список левых потомков и список правых потомков. Но это не единственные вырожденные деревья. Условием вырожденности дерева является наличие у любой вершины, кроме последней, только одного потомка. На рисунке 1 приведены все возможные вырожденные деревья для n = 4.

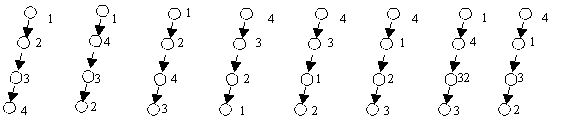
Рис.1. Примеры вырожденных деревьев

Идеальные деревья

    Как уже ясно, при данном n = 2^k-1 существует только одно идеальное бинарное дерево. Это должно обескураживать. Ведь вырожденных деревьев с тем же количеством вершин 2^(n-1). Значит ли это, что плохие деревья встречаются чаще, чем хорошие?

    Анализ ситуации основан на анализе последовательностей значений и на том, какие деревья порождаются последовательностями. Как известно, имеется n! различных последовательностей (перестановок) из n чисел. Это значительно больше, чем количество:

деревьев с n вершинами. Следовательно, некоторые перестановки порождают одинаковые деревья. В связи с единственностью идеального дерева вопрос должен быть сформулирован так: сколько различных последовательностей чисел при помещении этих чисел в бинарное дерево порождают идеальное дерево? Именно отношение числа таких последовательностей к общему числу различных последовательностей (n!) и характеризуют частоту появления идеальных деревьев.

    Конкретная последовательность диктует трассу алгоритма построения дерева. Все множество последовательностей, порождающих идеальные деревья, можно разделить на группы (подмножества) по типам трасс. Например, можно выделить группу последовательностей, строящих дерево по уровням: вершины не включаются в (i + 1)-й уровень, пока не завершен i-й уровень.

    Другая группа - заполнение дерева сначала левого поддерева, а затем правого и т. д. - непересекающихся групп может быть выделено очень много (две последовательности отличаются, если в них изменен порядок хотя бы двух чисел).

    Оценим количество последовательностей в первой группе - последовательностей, заполняющих дерево по уровням. Поскольку не для любого n существует идеальное дерево будем рассматривать только значения n = 2^k-1. Пусть даны n различных чисел, которые нужно поместить в дерево. Их конкретные значения не влияют на анализ, но для определенности возьмем числа 1, 2, 3, ..., n. Каждое из них имеет определенное место в идеальном дереве, например, в четырехуровневом дереве при n = 15 (рисунок 2).

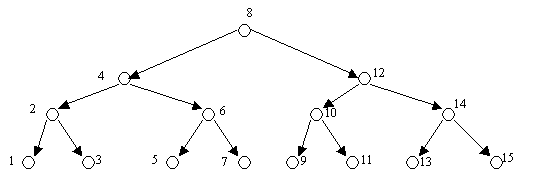
Рис.2. Идеальное четырехуровневое дерево

    Любая последовательность чисел 1, 2, 3, ..., 15 должна начинаться с 8, иначе построить дерево не удастся. Вторым членом последовательности может быть 4 или 12, третьим членом - то из двух чисел, которое не было выбрано в качестве второго члена. Четвертым членом может быть любое из чисел 2, 6, 10, 14, пятым - любое из трех, не выбранных в качестве четвертого и т. д.

    Рассматривая заполнение по уровням, можно заметить, что:

• на первом уровне выбора нет - имеется только одно число, 2^(k-1), которое должно стать корнем;
• на втором уровне имеется 2 вершины и 2! возможностей выбора второго и третьего элементов последовательности;
• на третьем уровне 4 вершины и 4! возможностей выбора четвертого ... седьмого элементов последовательности;
• на k-м уровне 2_(k-1) вершин и 2^(k-1)! возможностей выбора "хвоста" последовательности.

    Таким образом, общее количество вариантов построения последовательностей чисел, приводящих к идеальному графу при поуровневом заполнении, равно:

  (20)! (21)! (22)! (23)! ... (2k-1)!

    При k=2, n=3 имеется 2! = 2 последовательности поуровневого заполнения и это единственные последовательности, приводящие к идеальному дереву. Заметим, что вырожденных деревьев получается больше - 4. При k = 3, n = 7 получаем 1! 2! 4! = 48 последовательностей (общее количество последовательностей, приводящих к идеальному графу любыми способами, равно 80 - найдено прямым подсчетом). Вырожденных деревьев - 64.

    Картина резко меняется при дальнейшем увеличении n. Четыре уровня, n = 15: вырожденных деревьев - 34768; идеальных последовательностей - 1935360. Пять уровней, n = 31: вырожденных деревьев - 2147483648 ~ 2,15*10⁹; количество идеальных последовательностей 1,9*10²¹.

    Два последних примера показывают, что идеальные деревья могут встречаться гораздо чаще, чем вырожденные. Чтобы показать, что для достаточно больших n это всегда так, оценим отношение частот их появления; причем частоту появления идеальных деревьев оценим снизу, используя количество последовательностей, строящих дерево по уровням. Чуть менее громоздко формула будет выглядеть, если взять логарифм отношения частот. Факториалы, встречающиеся в формулах, заменим приближенными выражениями по формуле Стирлинга:

    Тогда логарифм отношения частот равен:

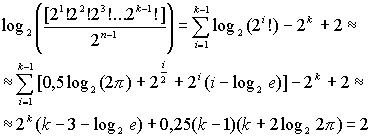
    В выводе последней формулы для упрощения выражения некоторые конечные суммы (геометрической прогрессии и др.) заменены бесконечными, что, учитывая быструю сходимость соответствующих рядов, дает относительно небольшую ошибку.

    Из этой формулы видно, что при k > 4 значение логарифма отношения частот положительно и, следовательно, идеальные деревья встречаются чаще вырожденных. Более того, значение логарифма быстро растет, увеличивая разрыв частот.

    К этому анализу необходимо добавить несколько замечаний. Во-первых, учтены были не все последовательности, порождающие идеальные деревья, т. е. на самом деле отношение частот еще больше. Во-вторых, идеальные и вырожденные деревья - это крайние случаи; между ними множество почти идеальных (заметим, что даже не для любого n существуют идеальные деревья) и почти вырожденных и некие средние случаи разреженных деревьев. В-третьих, реальный интерес при анализе сложности программ и алгоритмов имеют только случаи достаточно большого (сотни, тысячи и более) количества вершин в дереве, поэтому можно не прибегать к точным вычислениям, а использовать асимптотические оценки.

    Из приведенных выше результатов можно с достаточной степенью уверенности сделать следующий вывод: хорошие деревья получаются в результате включения случайных элементов существенно чаще, чем плохие; поэтому, средние оценки сложности операций поиска и включения вероятнее всего будут логарифмическими.

    На следующем шаге мы рассмотрим балансировку деревьев.

Предыдущий шаг Содержание Следующий шаг