На этом шаге мы рассмотрим рекурсивный алгоритм умножения матриц.

    Классический итеративный алгоритм перемножения квадратных матриц размера n*n имеет сложность O(n³), а нижняя оценка сложности не менее O(n²). Следовательно, оптимальный алгоритм имеет сложность, заключенную в этом узком коридоре. Отыскивая алгоритм в классе алгоритмов, разбивающих задачу на a подзадач в c раз меньшего размера с уравнением для функции сложности:

Т(n) = а Т(n/с) + bn^k, T(1) = b,

вспоминаем возможные оценки сложности O(n^k), O(n^klоg_cn), O(n^lоg_cn). Эти оценки были получены в предположении, что на один шаг разбиения задачи на a подзадач (без решения самих подзадач) требуется bn^k операций. Три оценки отражают три варианта соотношений между а и c^k: a < c^k, a = c^k, a > c^k.

    Поскольку хотим получить алгоритм с показателем функции сложности меньше трех, то не можем допустить в алгоритме ни одного шага со сложностью O(n³) или более. Следовательно, k может быть равно только единице или двум. При k = 1 отпадают два первых варианта (а < с¹, а = с¹), так как в этом случае получались бы оценки сложности ниже нижней границы O(n²). В третьем варианте с учетом нижней границы требуется, чтобы 2 <= log_cа < 3 или c² <= а < с³.

    Сделаем попытку применить рекурсию с использованием известного в теории матриц блочного представления:

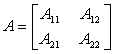
    Здесь A_ij - матрицы размера (n/2)*(n/2).

    Аналогично представим блоками матрицы В и С. Тогда произведение С=АВ можно найти в четыре этапа, вычислив блоки С₁₁, С₁₂, С₂₁, С₂₂ матрицы C по формулам C_ij = A_i,1B_1,j + A_i,2B_2,j.

    Рекурсивная процедура Перемножить вызывается с координатами левого верхнего угла (r_A - номер строки, c_A - номер столбца) матрицы A и с аналогичными координатами матриц В и С (при первом вызове все координаты равны единице), размером матриц n. В процессе выполнения процедура вызывает себя для перемножения блоков половинного размера. Для суммирования частных произведений она вызывает вспомогательную процедуру Сложить и использует вспомогательные матрицы XI и Х2 для хранения промежуточных результатов.

    Если размеры матриц n=1, то производится обычное умножение скалярных значений (элементов матриц).

процедура Перемножить (А, В: матрица; 
           переменная C: матрица; rА, сА, rВ, сВ, rС, сС: индекс; n: размер); 
           переменная X1, X2: матрица; 
начало 
      если n > 1 то
         начало 
           {Вычислить 1-й блок:} 
           Перемножить(A, В, XI, rА, сА, rВ, сВ, 1, 1, nil); 
           Перемножить(A, В, X2, rА, сA+n/2, rВ+n/2, сB, 1, 1, n/2); 
           Сложить (Х1, Х2, С, rС, cC, n/2); 
           {Вычислить 2-й блок:}
           Перемножить(A, В, XI, rА, сА, rВ, сВ+n/2, 1, 1, n/2); 
           Перемножить(A, В, Х2, rА, сA+n/2, rВ+n/2, сB+n/2,1,1,n/2);
           Сложить(Х1, Х2, С, rС, сC+n/2, n/2); 
           {Вычислить 3-й блок:}
           Перемножить(A, В, XI, rА+n/2, сA, rВ, cВ,1,1, n/2); 
           Перемножить (A, В, Х2, rА+n/2, сA+n/2, rВ+n/2, сB,1,1,n/2);
           Сложить(Х1, Х2, С, rС+n/2, cС, n/2); 
           {Вычислить 4-й блок:}
           Перемножить (A, В, XI, rА+n/2, cА, rВ, cВ+n/2,1,1,n/2);
           Перемножить (A, В, Х2, rА+n/2, cА+n/2, rВ+n/2, cВ+n/2,1,1, n/2);
           Сложить (Х1, Х2, С, rС+n/2, cC+n/2, n/2);
         конец
      иначе С[rС, cС]:= А[rА, cА] * В[rВ, cВ] {Умножение скаляров.}
конец

    Легко видеть, что для этой процедуры k=2, c=2, т. е. с^k = 4. Поскольку процедура вызывает себя восемь раз (a=8), то мы имеем вариант а > с^k и решение уравнения для функции сложности имеет вид O(n^log_ca) = O(n³).

    К сожалению, улучшения результата по сравнению с классическим алгоритмом не произошло. Улучшение возможно, если, оставаясь в рамках данного подхода, сумеем организовать вычисления таким образом, чтобы значение a было меньше восьми.

    Это удалось сделать в 1969 г. немецкому ученому Ф. Штрассену (Volker Strassen). В его методе а=7, т.е. сложность O(n^2,81). Ф.Штрассен предложил вычислять блоки матрицы-произведения следующим образом:

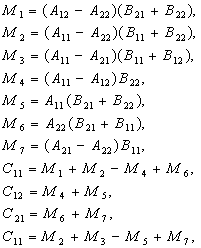
    В этих равенствах только семь умножений матриц, следовательно, рекурсивная процедура содержит в своем теле семь рекурсивных вызовов. Кроме того, имеется 18 аддитивных (сложений и вычитаний) матричных операций, но они не рекурсивны и имеют квадратичную сложность.

    Конечно, практическое значение алгоритм Штрассена вряд ли имеет, так как зависимость и 2,81 дает выигрыш против n³ только при очень больших размерностях задачи, а накладные расходы на организацию рекурсии и на дополнительные аддитивные матричные операции (в классическом алгоритме их четыре) велики. Но с теоретической точки зрения результат очень важен: он помогает продвинуться к пониманию того, какова сложность задачи.

    На следующем шаге мы рассмотрим задачу перемножения длинных целых чисел без знака.

Предыдущий шаг Содержание Следующий шаг