На этом шаге мы приведем общие сведения о методах разработки алгоритмов.
Заказчики (или конечные пользователи - end-users) ставят перед программистом задачу обычно следующим образом: "имеются исходные данные X; вычислительная машина должна выдать результаты Y, которые находятся в такой-то зависимости от исходных данных". Далее следует описание этой зависимости как некоторой функции или системы функций, возможно с дополнительными условиями, налагаемыми на вид результата.
Примеры задач.
- Даны матрица и вектор. Найти вектор, равный произведению матрицы на исходный вектор.
- Дана матрица. Определить, существует ли обратная матрица.
- Дана строка символов. Исключить из нее все символы, не являющиеся буквами или цифрами.
- Дана последовательность чисел. Найти минимальное из чисел.
- Дана последовательность чисел. Переписать ее (найти новую последовательность) так, чтобы числа располагались по возрастанию.
Приведенные формулировки задач просты, но их никак не назовешь описаниями алгоритмов. В этих формулировках отсутствуют такие свойства алгоритмов как элементарность шагов и дискретность. Каждое описание представляет собой формулировку одного шага: "дано - найти", но любой такой шаг не является элементарным - матрицы, строки и последовательности могут быть сколь угодно большими и ясно, что компьютеру потребуется неопределенно большое время, чтобы найти результат. Раз шаг всего лишь один и не тривиальный, то не выполняется и свойство дискретности, требующее указать последовательность шагов.
Со свойством массовости все проще - приведенные формулировки ориентированы на произвольные исходные данные, взятые из некоторых классов, т. е. свойство массовости выполняется. Определенность (детерминированность) также имеет место.
С конечностью (финитностью) имеется некоторая неопределенность. С одной стороны, раз шаг всего один, то алгоритм заканчивает свою работу через конечное число шагов. С другой стороны, это свойство нельзя рассматривать в отрыве от свойства элементарности шагов: единственный шаг может никогда не завершиться. Примером такого сорта задачи является задача, подобная той, что привел А.Рейтинг в книге "Интуиционизм": вычислить Y, исходя из условия: Y := 1, если в десятичном разложении числа n встречается последовательность 0123456789, и Y := 0 - в противном случае. Неизвестно, есть ли такая последовательность и сможем ли когда-нибудь найти решение этой задачи даже, если привлечем большие вычислительные мощности.
Таким образом, перед программистом стоит большая проблема - превратить описание задачи в описание алгоритма. Иначе говоря, один неопределенный шаг расписать в последовательность элементарных шагов.
Среди компьютерных наук существует одна, называемая "Технологией программирования", предметом которой и является разработка методов создания программных комплексов на основе описаний задач. В технологии программирования рассматриваются методы формализованного описания постановки задачи, входных и выходных данных (спецификации), методы повышения производительности труда программистов и повышения надежности работы программ (структурное и модульное программирование), приемы организации эффективной совместной работы нескольких программистов и др.
Здесь не будут рассмотрены все эти несомненно важные проблемы, обратимся исключительно к вопросам алгоритмизации задач. Попытаемся показать переход от "что надо сделать" к тому, "как это сделать".
Ключевым подходом в алгоритмизации является сведение задачи к подзадачам. Это естественно, так как предстоит превратить один шаг в последовательность элементарных шагов. Само это преобразование также может состоять из нескольких этапов, на которых единственный шаг разбивается на несколько более простых, но еще не элементарных. Эти более простые шаги соответствуют частным задачам (подзадачам), совокупное решение которых приводит к решению исходной задачи. Иерархию задач можно изобразить в виде дерева (рисунок 1).
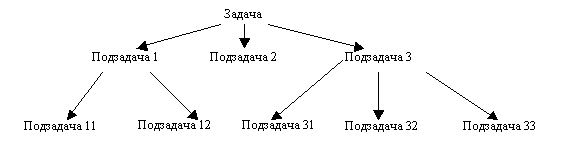
Рис.1. Иерархия задач
Различные методы разработки алгоритмов отличаются тем, на какие подзадачи производится разбиение и как эти подзадачи соотносятся между собой. Хотя нет общепринятой классификации методов разработки алгоритмов, тем не менее, некоторые общие соображения на этот счет могут быть высказаны.
Любая задача может быть сформулирована как функция преобразования исходных данных в выходные данные, f(X)=Y. Как исходные данные, так и функция могут быть достаточно сложными. Например, X - число, вектор, текст на каком-либо языке, база данных, рисунок, мультимедиа информация. То же можно сказать и о выходных данных. Функция может быть суммой чисел, тригонометрической функцией, корнем уравнения, переводом текста с русского на английский, раскраской полутонового рисунка, созданием спецэффектов в видеоинформации и т.д.
Разбивая задачу на подзадачи, можно:
- разбивать исходные и выходные данные на части или упрощать их; под разбиением понимаем разделение структуры данных на части, например, разделение вектора из десяти компонент на два вектора по пять компонент или разделение текста на предложения; под упрощением понимаем такие ситуации, когда, например X - число и его нельзя разбить на части, но его можно разложить, скажем, в сумму X = X1 + X2, так, что результаты f(X1), f(X2) отыскиваются проще, чем f(X);
- производить декомпозицию функции, т. е. превращать ее в суперпозицию более простых,
f(Х) = g(h(s(X))) илиf(Х) = g(X, h(X), s(X)) .
При разработке алгоритма может систематически использоваться первый подход, систематически использоваться второй подход или могут совместно использоваться оба подхода.
На следующем шаге мы рассмотрим разложение задачи в последовательность разнородных подзадач.
