На этом шаге мы рассмотрим метод Лагранжевых релаксаций.

    В начале 70-х годов была высказана идея[1, 2], которая в последствии оказалась очень продуктивной при решении дискретных экстремальных задач. Многие NP-трудные задачи можно представить как "легкие" задачи с дополнительными отягощающими ограничениями. Лагранжевы релаксации получаются путем перехода к двойственной задаче относительно этого множества дополнительных ограничений. Релаксированная задача уже легко решается и ее оптимальное решение дает оценку снизу (в задачах на минимум) для целевой функции исходной задачи. Если разрыв двойственности равен нулю, то такой подход дает возможность найти оптимальное решение задачи и доказать его оптимальность. В противном случае, когда полученная нижняя оценка не является точной, она может быть использована в методе ветвей и границ или (и) служить начальным приближением для эвристических методов[3, 4].

    Использовать множители Лагранжа в задачах дискретной оптимизации впервые предложил Эверетт[5] в 1963 году. Однако бум в этой области начался после выхода в свет работы Хэлда и Карна[6], посвященной задаче коммивояжера. Эта работа послужила толчком для теоретических и прикладных исследований в данной области. В 1973 г. выходит в свет работа Фишера[7], в которой этот подход используется для задач теории расписаний. В этом же году появляется статья Шапиро и Фишера[8], в которой метод Лагранжевых релаксаций развивается применительно к общей задаче целочисленного программирования. Сам термин Лагранжева релаксация был предложен Джеоффрионом[9]. В этой статье, написанной, по выражению автора, с педагогическими целями, сформулированы и доказаны основные теоремы. Однако центральный вопрос: "Каким образом вычислять множители Лагранжа?" - оставался открытым. В 1975 г. Фишер, Норшип и Шапиро[10] дали подробные теоретические разъяснения по этому поводу, а Хэлд, Волф и Краудер[11] дали конкретные практические рекомендации. В 1979 г. Шапиро[1] публикует обзор, в котором содержится обширная библиография по применению техники Лагранжевых релаксаций в задачах целочисленного программирования. В 1981 г. выходит аналогичный обзор Фишера[2]. К настоящему времени этот метод детально разработан и опробован для задач размещения, расписаний, назначений и др.

    Пусть множество ограничений исходной задачи P разбито на две части:

  P:   min cx
       Ax >= b, Bx >= d
       x >= 0, целые

    Под Лагранжевой релаксацией с множителями λ>=0 будем понимать задачу вида:

LR(λ):  min cx + λ(b - Ax)
           Bx >= d
           x  >= 0, целые. 

    Задача, двойственная к задаче P относительно ограничений Ax>=b, по определению есть задача вида:

  D: max v(LP(λ)),
       λ>=0, 

где v(LP(λ)) - оптимальное значение соответствующей релаксированной задачи LP(λ). В общем случае v(P)>=v(D), но величина v(D) может существенно зависить от разбиения системы ограничений на части. Заметим, что эти части могут пересекаться.

    Среди методов решения задачи D наибольшее распространение получили методы субградиентной оптимизации. Эти итеративные процедуры формируют последовательность векторов {λ^k}. Начиная с некоторого начального значения λ⁰ эти вектора меняются по следующему правилу:

λ_k+1 = λ^k + t_k (A x^k - b),

где x^k - оптимальное решение задачи , а t_k - размер шага. Фундаментальный теоретический результат заключается в том, что[12]:

    Размер шага на практике обычно выбирают следующим[11]:

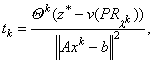
где θ^k - скаляр, 0 < θ^k<= 2 и z^* - верхняя граница для v(D). Обычно z^* получают эвристикой для P. В методе ветвей и границ z^* - текущий рекорд. Последовательность θ^k, как правило, начинается с θ⁰=2 и затем θ^k делится пополам, через фиксированное число итераций, зависящее от размерности задачи.

Предыдущий шаг Содержание