На этом шаге мы рассмотрим класс сложности задач NP.
Изобразим условно взаимоотношение классов задач полиномиальной и экспоненциальной сложностей (рисунок 1).
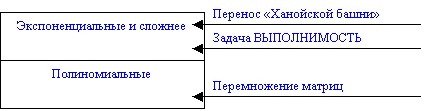
Рис.1. Сложность некоторых задач
Здесь каждая точка области, ограниченной прямоугольником, представляет некоторую задачу. Две точки - это примеры задач из разных классов. Выше было выяснено, что для переноса "Ханойской башни" требуется O(2n) операций, а для перемножения матриц не более, чем O(n3) операций. О третьей точке - задаче ВЫПОЛНИМОСТЬ - речь пойдет ниже.
Где проходит граница между классами задач полиномиальной сложности P и экспоненциальной сложности ЕХР? Ответ на этот вопрос, т. е. описание границы (например, задачи с такими-то свойствами входят в класс P, а все остальные входят в класс ЕХР) в настоящее время не известен. Чтобы разведать границу, математики придумали еще один класс задач - NP. Интуитивно предполагается, что он может оказаться "нарушителем границы". Это класс задач, которые можно решить за полиномиальное время (P), но на машине, более мощной, чем обычная однопроцессорная машина - на недетерминированном (N) вычислителе. Недетерминированный вычислитель исполняет так называемые недетерминированные алгоритмы. Напомним свойство детерминированности: определенность (детерминированность) алгоритма означает, что для каждого шага могут быть по набору исходных для шага данных однозначно вычислены результаты выполнения шага, и эти результаты не зависят ни от каких случайных факторов. Соответственно этому и алгоритм в целом по окончании работы исполнителя выдает вполне определенный результат.
Недетерминированный алгоритм лишен этого свойства. Разрешаем шаги с неоднозначным результатом - шаги, вырабатывающие сразу несколько значений для одной и той же переменной. Эти несколько значений далее могут быть использованы одним из двух способов.
Первый способ. Создать несколько параллельно выполняющихся процессов (по процессу для каждого значения) для продолжения вычислений. Это возможно на многопроцессорной машине с неограниченно большим количеством параллельно работающих процессоров.
Насколько серьезно может помочь распараллеливание в ускорении решения задачи? Является ли многопроцессорная машина панацеей? Может быть, не стоит тратить силы на совершенствование технологий микроэлектроники и пытаться увеличивать скорость работы процессора, может быть, остановиться на тех процессорах, которые уже разработаны, и пойти по пути увеличения количества процессоров в вычислительной системе?
Рассмотрим в качестве примера задачу вычисления суммы n чисел ai. На однопроцессорной машине для ее решения потребуется выполнить (n-1) операций сложения. Если у нас имеется неограниченное количество процессоров, то на первом шаге можем параллельно выполнить попарные сложения a1 + a2, a3 + a4, ... . Затем результаты первого шага снова подвергнуть попарному сложению и т. д. На каждом шаге количество слагаемых будет уменьшаться в два раза по отношению к предыдущему шагу (при четном количестве слагаемых на предыдущем шаге) пока не дойдет до одного слагаемого. Это и будет результатом. Нетрудно подсчитать, что нам потребуется порядка log2n шагов. Существенное ускорение за счет распараллеливания, но все-таки не 100% - все не было сведено к одному шагу.
Второй способ. Угадать, какое из нескольких значений, полученных на данном шаге, является правильным (задающим искомое решение) и использовать в дальнейшем только его, игнорируя все остальные. В этом случае требуется только один процессор, но дополненный угадывающим устройством.
С точки зрения теории сложности не важно, каким именно из двух способов производить вычисление (временная сложность одинакова). Первый способ соответствует дереву возможностей и параллельному движению по всем ветвям дерева, а второй способ состоит в угадывании того, по какой ветви нужно двигаться и в движении по угаданной ветви. В дальнейшем будут продемонстрированы в доказательствах теорем оба варианта недетерминированного вычислителя.
Важным примером задачи из класса NP является задача ВЫПОЛНИМОСТЬ.
Рассмотрим детальнее проблему выполнимости для пропозиционального исчисления (раздела математической логики), так как она была одной из первых проблем в исследовании класса NP. Кроме того, любая задача может быть сформулирована либо как утверждение, истинность которого нужно проверить, либо как предикат (утверждение, включающее свободные переменные), для которого нужно найти значения свободных переменных, дающие получающемуся из предиката утверждению значение "истина". Поскольку пропозициональное исчисление близко тому, что в курсе "Дискретная математика" называется булевой алгеброй, рассмотрим эту задачу в терминах булевой алгебры.
Пусть Φ(x1, x2 ..., xn) - формула булевой алгебры, представленная в конъюнктивной нормальной форме (КНФ):
Φ(x1, x2, ..., xn) = & Di ,
Di = ∨ 
(σj = 0 или 1). Часть формулы, обозначенная Di,
называется дизъюнктом, а часть формулы, записанная как ,
называется литералом. Таким образом, литерал - это переменная или ее отрицание. В дизъюнкт могут
входить только некоторые из n переменных (не обязательно все). Пример КНФ:
Здесь знак ¬ обозначает отрицание, т. е. ¬x = х0.
Длина дизъюнкта - количество литералов в дизъюнкте. В приведенном примере имеются четыре дизъюнкта с длинами 2, 3, 1, 2.
Булева формула (выражение) называется выполнимой, если существует хотя бы один набор значений {аi} такой, что Φ(a1, a2, ..., an)=1. Решение задачи о выполнимости состоит в ответе на вопрос, является ли заданное в форме КНФ выражение выполнимым.
С алгоритмической точки зрения для решения задачи нужно построить процедуру, которая воспринимала бы на входе строку символов длиной n - слово в алфавите (&, ∨, (, ), x1, x2, ..., xn), являющееся записью выражения Е, и по окончании работы выдавала один из двух ответов: "выполнимо" или "не выполнимо". Сложность такой процедуры является функцией сложности исходных данных n.
На следующем шаге мы рассмотрим теорему о принадлежности задачи ВЫПОЛНИМОСТЬ классу NP.
