На этом шаге мы рассмотрим еще один однократный поворот.

    Этот алгоритм ничем не отличается от рассмотренного на предыдущем шаге, только поворот осуществляется в другую сторону.

    Приведем текст алгоритма:

    p1 = (*p).Right;
    (*p).Right = (*p1).Left;
    (*p1).Left = p; 
    (*p).bal = 0; p = p1;

    Рассмотрим его использование на конкретном примере.

    Пусть дано следующее дерево:

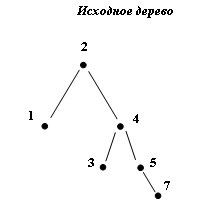
Рис.1. Исходное дерево

    Иллюстрируем алгоритм с помощью схем "до и после" Д.Кнута:

1. Определяем адрес той вершины, которая станет корнем дерева:

       p1 = (*p).Right;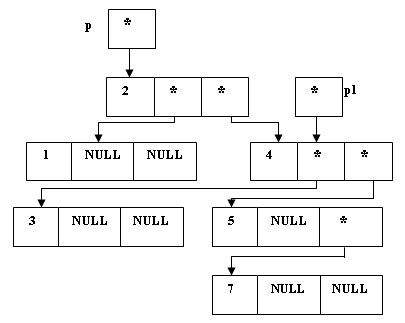
   

   
   Рис.2. Сохранение адреса нового корня дерева

2. Переприкрепляем левое поддерево от "нового" корня, делая это поддерево правым поддеревом "старого" корня:

       (*p).Right = (*p1).Left;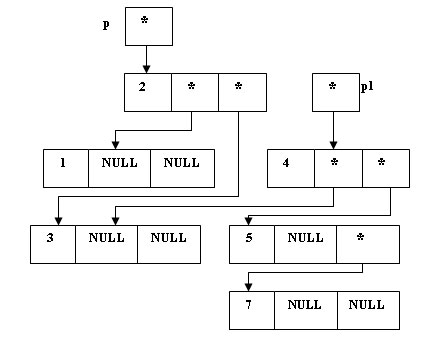
   

   
   Рис.3. Переприкрепление

3. Определяем левое поддерево "нового" корня, как начинающееся со "старого" корня:

       (*p1).Left = p;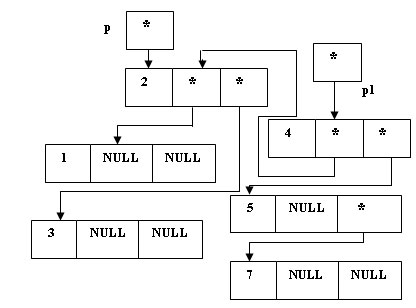
   

   
   Рис.4. Определение левого поддерева "нового" корня

4. Изменяем значение указателя на корень дерева (p) и обнуляем значение сбалансированности:

       (*p).bal = 0; p = p1;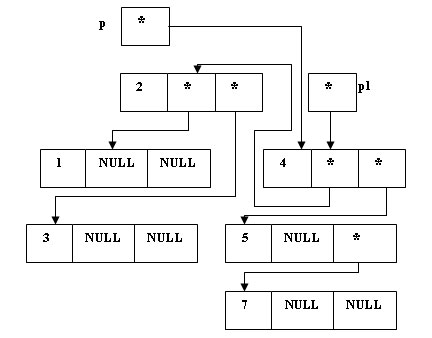
   

   
   Рис.5. Установка начальных значений

    В результате получилось следующее сбалансированное дерево:

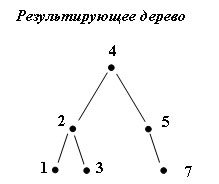
Рис.6. Результат балансировки

Вывод.

Если после вставки показатели сбалансированности вершин имеют одинаковый знак и отличаются только на единицу, то восстановить баланс дерева можно однократным поворотом (включая одно "переприкрепление" поддерева), при этом вставка не будет оказывать влияния на другие участки дерева.

    Проиллюстрируем эту несбалансированность и ее устранение следующими рисунками:

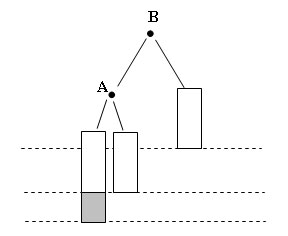
Рис.7. Несбалансированность (отмечен узел, вызвавший несбалансированность)

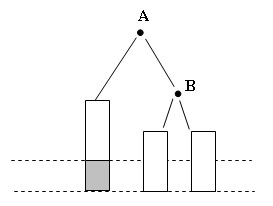
Рис.8. Несбалансированность устранена (отмечен узел, вызвавший несбалансированность)

    Со следующего шага мы начнем рассматривать двухкратные повороты.

Предыдущий шаг Содержание Следующий шаг