На этом шаге мы рассмотрим первый двухкратный поворот.

    На этом и следующем шагах мы приведем алгоритмы двухкратных поворотов, проиллюстрируем их конкретными примерами и в конце следующего шага сформулируем общее правило их использования.

    Итак, приведем текст алгоритма:

    p1 = (*p).Left; p2 = (*p1).Right;
    (*p1).Right = (*p2).Left; (*p2).Left = p1;
    (*p).Left = (*p2).Right; (*p2).Right = *p;
    p = p2; 

    Рассмотрим его использование на конкретном примере.

    Пусть дано следующее дерево:

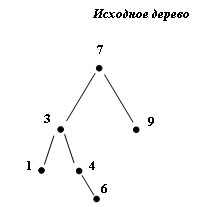
Рис.1. Исходное дерево

    Иллюстрируем алгоритм с помощью схем "до и после" Д.Кнута:

1. Определим p1 как указатель на левое поддерево, а p2 как указатель на правое поддерево дерева p1:

       p1 = (*p).Left; p2 = (*p1).Right;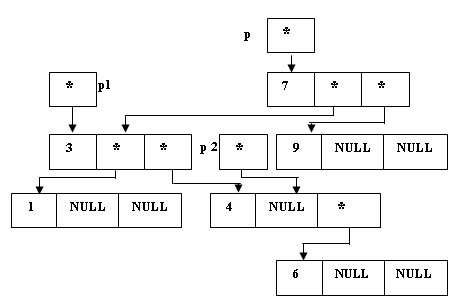
   

   
   Рис.2. Определение p1 и p2

2. Переприкрепляем левое поддерево дерева p2 на место правого поддерева дерева p1:

       (*p1).Right = (*p2).Left;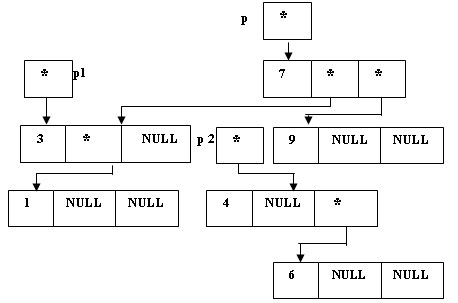
   

   
   Рис.3. Переприкрепление

3. Определяем левое поддерево "нового" корня p2, как начинающееся с p1:

       (*p2).Left = p1;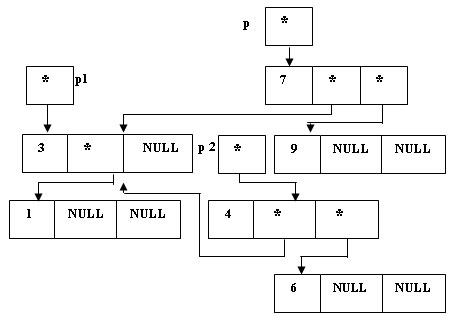
   

   
   Рис.4. Определение левого поддерева "нового" корня

4. Переприкрепляем правое поддерево дерева p2 на место левого поддерева "старого" корня:

       (*p).Left = (*p2).Right;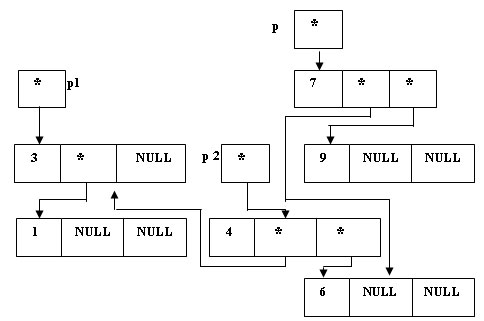
   

   
   Рис.5. Переприкрепление

5. Определяем правое поддерево "нового" корня p2, как начинающееся со "старого" корня:

       (*p2).Right = *p;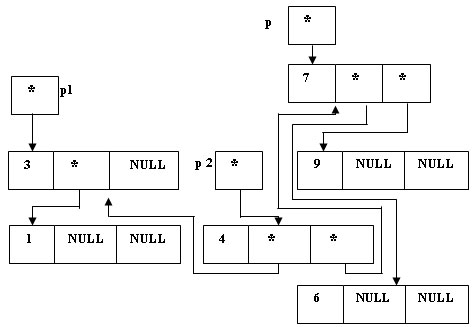
   

   
   Рис.6. Определение правого поддерева "нового" корня

6. Изменяем значение указателя на корень дерева (p):

       p = p2;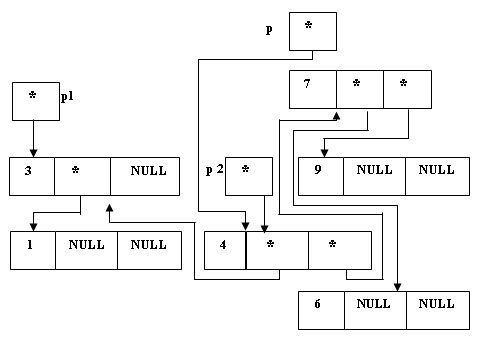
   

   
   Рис.7. Установка начальных значений

    В результате получилось следующее сбалансированное дерево:

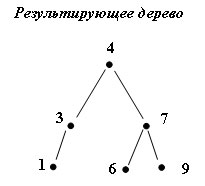
Рис.8. Результат балансировки

    На следующем шаге мы рассмотрим второй двухкратный поворот.

Предыдущий шаг Содержание Следующий шаг