Шаг 81.
Реализация простейших операций над графами, представленными списками смежности

    На этом шаге мы рассмотрим несколько операций над графами, представленными списками смежности.

    Теперь приведем реализацию на языке C++ простейших операций над графами с использованием представления графов списками смежности.

    Вначале опишем типы данных: 

#define N 12; // Количество вершин графа.
typedef struct zveno *svqz;
typedef struct zveno 
{
  int Key; //Вершина графа.
  svqz Sled; // Указатель на следующую смежную вершину.
 } Leader;
svqz beg[N]; // Описание типа списков смежности.

    1. Построение списков смежности, соответствующих данному ориентированному графу. Перед первым обращением к функции MakeGraph (создание графа) необходима инициализация списков смежности: 

    for (i=0;i<N;i++) beg[i] = NULL;

void MakeGraph (svqz beg[N])
// Построение списков смежности beg графа.
{
  int x,y;
  svqz ukzv,uzel; //Рабочие указатели.

  cout<<"Вводите начало дуги: "; 
  cin>>x;
  while (x!=0)
  {
    cout<< "Вводите конец дуги: ";
    cin>>y;
    AddGraph (x,y,beg);
    cout<< "Вводите начало дуги: "; cin>>x;
  }
}

    2. Вывод содержимого списков смежности, соответствующих ориентированному графу. 

void PrintGraph (svqz beg[N])
{
  int i;
  svqz ukzv; //Рабочий указатель.
  for (i=1;i<N;i++)
  { 
    cout<<i<<" ..."; 
    ukzv = beg[i]; 
    if (ukzv==NULL) cout<<"Пустой список!\n"; 
    else { 
      while (ukzv!=NULL) 
        { cout<< (*ukzv).Key; ukzv = (*ukzv).Sled; } 
      cout<<endl; }
  }
}

    Теперь рассмотрим реализацию унарных операций [1, с.22] на графе.

    3. Добавление дуги (x,y) (если ее не было!) к спискам смежности, соответствующим ориентированному графу. 

void AddGraph (int x, int y, svqz beg[N])
{
  svqz ukzv,uzel; //Рабочие указатели.
  if (beg[x]!=NULL)
  { 
    Poisk (beg[x],y,&ukzv); 
    if (ukzv==NULL) 
    { // Добавление элемента в конец списка, 
       // заданного указателем beg[x]. 
      uzel = new (Leader); 
      (*uzel).Key = y; (*uzel).Sled = NULL; ukzv = beg[x]; 
      while ((*ukzv).Sled!=NULL) 
        ukzv = (*ukzv).Sled;
      (*ukzv).Sled = uzel; 
    }
  }
  else
  {
    beg[x] = new (zveno);
    (*beg[x]).Key = y; (*beg[x]).Sled = NULL;
  }
}

    4. Удаление дуги между двумя заданными вершинами графа, представленного списками смежности (заметим, что вершины, инцидентные дуге, из графа не удаляются). 

void DeleteGraph (int x, int y, svqz beg[N])
{
  svqz ukzv;

  if (beg[x]!=NULL)
  //Удаление звена из списка без заглавного звена.
  { //Вершины в графе есть.
    Poisk (beg[x],y,&ukzv); 
    if (ukzv!=NULL) Udalenie (&beg[x],&ukzv); 
    else cout<<"Такой дуги в графе нет!\n";
  }
  else cout<<"Список пуст!\n";
} 

void Poisk (svqz uksp, int ment, svqz *res)
// Поиск звена с информационным полем ment в 
// однонаправленном списке uksp. *res - указатель 
// на найденное звено или NULL.
{
  svqz q;

  *res = NULL; q = uksp;
  while ((q!=NULL)&&(*res==NULL))
    { if ((*q).Key==ment) *res = q; 
      q = (*q).Sled; }
}

void Udalenie (svqz *ukstr, svqz *zv)
// Удаление звена, на которое ссылается указатель *zv, 
// из однонаправленного списка, заданного указателем *ukstr.
{
  svqz ukzv,z;

  if (((**ukstr).Sled==NULL)&&(*zv==*ukstr))
  // В списке - один элемент! 
    { *ukstr = NULL; delete zv; }
  else 
    if (*zv==*ukstr) // Удаляемый элемент - первый.
      { *ukstr = (**ukstr).Sled; delete zv; } 
    else { 
      z = *ukstr; ukzv = (**ukstr).Sled;
      while (ukzv!=*zv) 
        { z = ukzv; ukzv = (*ukzv).Sled; } 
      (*z).Sled = (*(*zv)).Sled; delete zv; 
  }
}

    Отметим, что удаление вершины v из графа G приводит к подграфу, содержащему все вершины графа G за исключением v, и все ребра графа G, не инцидентные v. Заметим, что при данном представлении графа удаление вершин становится достаточно громоздким.

    Приведем программу, демонстрирующую работу перечисленных выше функций.

    Пример. Построение списков смежности, соответствующих ориентированному графу, вывод их на экран, добавление и удаление дуг. 
#include <iostream.h>
#define N 12 //Количество вершин графа.
#define TRUE 1
#define FALSE 0

typedef struct zveno *svqz;
typedef struct zveno 
{
  int Key; //Вершина графа.
  svqz Sled; //Указатель на следующую смежную вершину.
 } Leader;

class Spisok {
  private:
    svqz beg[N]; //Описание типа списков смежности.
    svqz res; //Указатель на найденное звено.
    void Poisk (svqz,int);
    void Udalenie (svqz *);
  public:
    Spisok ();
    svqz GetPoisk () { return res; }
    void MakeGraph ();
    void AddGraph (int,int);
    void DeleteGraph (int,int);
    void PrintGraph ();
};

void main ()
{
  Spisok A;
  int x; // Начало дуги.
  int y; // Конец дуги.

  A.MakeGraph (); // Построение списков смежности.
  // Вывод списков смежностей.
  cout<<"Представление графа списками смежности\n";
  A.PrintGraph (); cout<<endl;
  // Добавление дуги к графу.
  cout<<"Добавим к графу новую дугу...\n";
  cout<<"Введите начало дуги: "; cin>>x;
  cout<<"Введите конец дуги: "; cin>>y;
  A.AddGraph (x,y);
  cout<<"Представление графа списками смежности\n";
  A.PrintGraph (); cout<<endl;
  //Удаление дуги из графа.
  cout<<"Удалим из графа заданную дугу...\n";
  cout<<"Введите начало дуги: "; cin>>x;
  cout<<"Введите конец дуги: "; cin>>y;
  A.DeleteGraph (x,y);
  cout<<"Представление графа списками смежности\n";
  A.PrintGraph (); cout<<endl;
} 

void Spisok::Poisk (svqz uksp,int ment)
// Поиск звена с информационным полем ment в 
// однонаправленном списке uksp. res - указатель
// на найденное звено или NULL.
{
  svqz q;

  res = NULL; q = uksp;
  while ((q!=NULL)&&(res==NULL))
    { if ((*q).Key==ment) res = q; q = (*q).Sled; }
} 

void Spisok::AddGraph (int x,int y)
// Добавление дуги (x,y) (если ее не было!) в граф,
// представленный списками смежности beg .
{
  svqz ukzv,uzel; // Рабочие указатели.

  if (beg[x]!=NULL)
  { 
    Poisk (beg[x],y); 
    if (GetPoisk()==NULL) 
      { //Добавление элемента в конец списка, заданного указателем beg[x].
        uzel = new (Leader); 
        (*uzel).Key = y; (*uzel).Sled = NULL; ukzv = beg[x]; 
        while ((*ukzv).Sled!=NULL) 
           ukzv = (*ukzv).Sled; 
        (*ukzv).Sled = uzel; }
  }
  else { beg[x] = new (zveno);(*beg[x]).Key = y; (*beg[x]).Sled = NULL; }
} 

void Spisok::MakeGraph ()
// Построение списков смежности beg графа.
{
  int x,y;

  cout<<"Вводите начало дуги: "; cin>>x;
  cout<<"Вводите конец дуги: "; cin>>y;
  while (x!=0)
  { 
    AddGraph (x,y);
    cout<< "Вводите начало дуги: "; cin>>x;
    cout<<"Вводите конец дуги: "; cin>>y;
  }
}

void Spisok::Udalenie (svqz *ukstr)
//* Удаление звена, на которое ссылается указатель res,
// из однонаправленного списка, заданного указателем *ukstr 
{
  svqz ukzv,z;

  if (((**ukstr).Sled==NULL)&&(res==*ukstr)) //В списке - один элемент! 
    { *ukstr = NULL; delete res; }
  else if (res==*ukstr) // Удаляемый элемент - первый.
        { *ukstr = (**ukstr).Sled; delete res; } 
       else { 
         z = *ukstr; ukzv = (**ukstr).Sled; 
         while (ukzv!=res) { z = ukzv; ukzv = (*ukzv).Sled; }
         (*z).Sled = (*res).Sled; delete res; }
}

void Spisok::DeleteGraph (int x,int y)
// Удаление дуги (x,y) из списков смежности beg.
{
  if (beg[x]!=NULL)
  // Удаление звена из списка без заглавного звена.
  { // Вершины в графе есть.
    Poisk (beg[x],y); 
    if (GetPoisk()!=NULL) Udalenie (&beg[x]); 
    else cout<<"Такой дуги в графе нет!\n"; }
  else cout<<"Список пуст!\n";
} 

void Spisok::PrintGraph ()
{
  svqz ukzv; // Рабочий указатель.

  for (int i=1;i<N;i++)
  { cout<<"..."<<i; ukzv = beg[i]; 
    if (ukzv==NULL) cout<<" Пустой список!\n";
    else { 
      while (ukzv!=NULL) { cout<<(*ukzv).Key; ukzv = (*ukzv).Sled; } 
      cout<<endl; }
  }
}

Spisok::Spisok() { for (int i=0;i<N;i++) beg[i] = NULL; }
Текст этой программы можно взять здесь.

    Во многих алгоритмах необходимо динамически модифицировать структуру неориентированного графа путем добавления и удаления ребер. Если это нужно выполнить достаточно быстро, то полагаем, что в списках смежности элемент списка beg[u], содержащий вершину v, снабжен указателем на элемент списка beg[v], содержащий вершину u (и наоборот!), что схематически можно изобразить так:


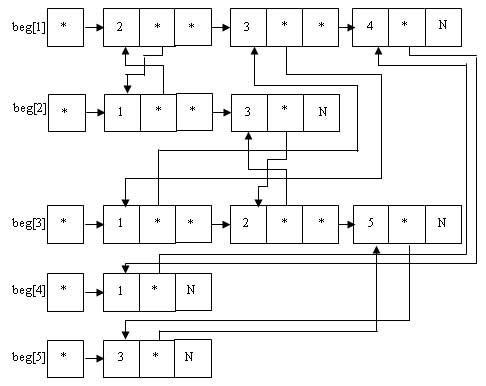
Рис.1. Представление графа

    Тогда, удаляя "часть" ребра (x,y) из списка, мы можем легко за число шагов, ограниченное константой, удалить другую "часть" ребра, а именно: (y,x), не просматривая весь список beg[y].

    Далее, можно еще более усложнить структуру, если предположить, что каждый список смежных вершин является двунаправленным (попробуйте изобразить это схематически!).

    Замечания.
  1. Аналогичным образом можно определить для каждой вершины v ориентированного графа список, определенный указателем SUC[v], содержащий вершины из множества {u: u->v}. "Еще один способ состоит в том, что для каждой вершины выписываются номера следующих, не смежных с ней..." [2, с.32].
  2. Представление графа в виде списков смежности определяет "порядок" ребер, смежных некоторой вершине графа. Граф с подобным упорядочиванием ребер называют упорядоченным графом. Дадим формальное определение.

       

    Определение 1 [3, с.237].
    Множество V={v1,v2,...,vn} вершин вместе с множеством {Lv1, Lv2,...,Lvn} упорядоченных списков упорядоченных пар вершин называют упорядоченным графом.

        Упорядоченный граф определяет единственный неупорядоченный граф. Обратное утверждение неверно, поскольку в общем случае возможно много способов упорядочения графа.

       

    Определение 2 [3, с.248].
    Упорядоченным ориентированным графом называется пара G=(V,E), где V - конечное множество вершин, а E - множество упорядоченных списков дуг. Элементы E имеют вид Lv=((v,w1),(v,w2),...,(v,wk)), где v,wi принадлежат V.

   

(1) Свами М., Тхуласираман К. Графы, сети и алгоритмы. - М.: Мир, 1984. - 454 с.
(2) Зыков А.А. Основы теории графов. М.: Наука, 1987. - 384 с.
(3) Кук Д., Бейз Г. Компьютерная математика. - М.: Наука, 1990. - 384 с.

    На следующем шаге мы рассмотрим представление графов с помощью ортогональных списков смежности.




Предыдущий шаг Содержание Следующий шаг