На этом шаге мы рассмотрим представление графов с помощью орогональных списков смежности.
На рисунке, приведенном ниже, изображен граф и его представление с помощью структуры данных, которую мы будем называть ортогональными списками смежности.
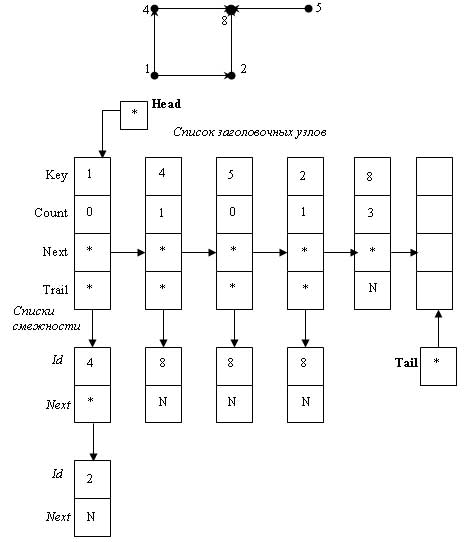
Рис.1.Ортогональные списки смежности
Вершины графа находятся в связанном списке, который называется списком заголовочных узлов. Каждый узел этого списка содержит четыре поля.
Если указатель P указывает на заголовочный узел, представляющий вершину Q графа, то:
- поле (*P).Key содержит информацию, связанную с этой вершиной Q;
- поле (*P).Count содержит количество вершин, "предшествующих" данной;
- поле (*P).Next содержит указатель на заголовочный узел, представляющий следующую вершину графа (если такая вершина есть) в списке заголовочных узлов;
- каждый заголовочный узел является заглавным звеном списка узлов второго типа, называемых дуговыми узлами. Такой список мы также будем называть списком смежности. Каждый узел списка смежности представляет конечную вершину некоторой дуги графа. Поле (*P).Trail указывает на список смежности, представляющий дуги, выходящие из вершины Q графа (английское слово "Trail" переводится как "тащиться, свисать, волочиться").
Каждый узел списка смежности содержит два поля: Id и Next, причем если Q указывает на списочный узел, представляющий дугу (A,B), то:
- поле (*Q).Id содержит вершину B графа;
- поле (*Q).Next указывает на дуговой узел, представляющий следующую дугу, выходящую из вершины A графа (если такая дуга есть).
На рисунке 1 показан граф и представление его ортогональными списками смежности. Каждый дуговой узел содержится в единственном списке смежности, представляющем все дуги, выходящие из данной вершины графа. Термин распределенные узлы используется как для заголовочных, так и для дуговых узлов структуры со многими связями, представляющей граф.
Приведем реализацию на языке C++ простейших операций над графами с использованием представления графов в виде ортогональных списков смежности.
Вначале опишем типы данных:
typedef struct L *Lref; // Тип: указатель на заголовочный узел. typedef struct T *Tref; // Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; // Имя заголовочного узла. int Count; //Количество предшественников. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; typedef struct T //Описание типа дугового узла. { int Id; Tref Next; } Trailer;
Приведем программу, демонстрирующую работу функций, предназначенных для выполнения некоторых операций над графами.
Пример. Построение ортогональных списков смежности, соответствующих ориентированному графу, вывод на экран структуры ортогональных списков смежности, добавление и удаление дуг, добавление и удаление вершин.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; //Тип: указатель на заголовочный узел. typedef struct T *Tref; //Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. Tref Trail; //Указатель на список смежности. Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; typedef struct T //Описание типа дугового узла. { int Id; Tref Next; } Trailer; class Spisok { private: Lref Head; //Указатель на начало списка заголовочных узлов. Lref Tail; //Указатель на фиктивный узел // в конце списка заголовочных узлов. void SearchGraph (int, Lref *); void Search (int, Lref *); public: Spisok () {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } void MakeGraph (); void AddGraph (int, int); void DeleteGraph (int, int); void PrintGraph (); void DeleteY (int); }; void main () { Spisok A; int x,y; //Начало и конец дуги //Построение и вывод структуры ортогональных списков. A.MakeGraph (); A.PrintGraph (); cout<<endl; //Добавление дуги к графу. cout<<"Добавим к графу новую дугу...\n"; cout<<"Введите начало дуги: "; cin>>x; cout<<"Введите конец дуги: "; cin>>y; A.AddGraph (x,y); A.PrintGraph (); cout<<endl; //Удаление дуги из графа. cout<<"Удалим из графа заданную дугу...\n"; cout<<"Введите начало дуги: "; cin>>x; cout<<"Введите конец дуги: "; cin>>y; A.DeleteGraph (x,y); A.PrintGraph (); cout<<endl; //Удаление вершины графа. cout<< "Введите удаляемую вершину: "; cin>>y; A.DeleteY (y); A.PrintGraph (); cout<<endl; } void Spisok::Search (int w, Lref *h) //Функция возвращает в *h указатель на заголовочный узел //ключом w. Если узел отсутствует, то функция возвращает NULL . { *h = Head; (*Tail).Key = w; //Поиск "с барьером". while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. *h = NULL; } void Spisok::SearchGraph (int w,Lref *h) //Функция возвращает в *h указатель на заголовочный узел //с ключом w. Если заголовочный узел отсутствует, то он //добавляется в список. { *h = Head; (*Tail).Key = w; while ((**h).Key!=w) *h = (**h).Next; if (*h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка *Head. { Tail = new (Leader); (**h).Count = 0; (**h).Trail = NULL; (**h).Next = Tail; } } void Spisok::MakeGraph () //Функция возвращает указатель Head на ортогональные //списки смежности, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; // Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? SearchGraph (x,&p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==y) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = y; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::AddGraph (int x,int y) //Добавление дуги (x,y) (если ее не было!) к связанной //структуре, соответствующей ориентированному графу Head. { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. //Определим, существует ли в графе дуга (x,y)? SearchGraph (x,&p); SearchGraph (y,&q); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==y) Res = TRUE; else r = (*r).Next; if (!Res) { //Если дуга отсутствует, то поместим её в граф. t = new (Trailer); (*t).Id = y; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; } } void Spisok::DeleteGraph (int x,int y) //Функция возвращает указатель Head на связанную //структуру, соответствующую ориентированному графу //и полученную удалением дуги (x,y). { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. //Определим, существует ли в графе дуга (x,y)? Search (x, &p); Search (y, &q); if ((p!=NULL)&&(q!=NULL)) { //Вершины x и y в графе есть. r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==y) Res = TRUE; else r = (*r).Next; if (Res) //Если дуга существует, то удалим её. if (r==(*p).Trail) { (*p).Trail = (*(*p).Trail).Next; delete r; (*q).Count--; } else { t = (*p).Trail; while ((*t).Next!=r) t = (*t).Next; (*t).Next = (*(*t).Next).Next; delete r; (*q).Count--; } } } void Spisok::PrintGraph () //Вывод структуры смежности, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<"("<<(*p).Key; q = (*p).Trail; while (q!=NULL) { cout<<(*q).Id; q = (*q).Next; } cout<<")"; p = (*p).Next; cout<<" "; } } void Spisok::DeleteY (int y) //Функция возвращает указатель Head на связанную струк- //туру, соответствующую графу с удаленной вершиной y. { Lref p,q; //Рабочие указатели. Tref r,s; //Рабочие указатели. int x; //Рабочая переменная. //Удаление всех дуг (x,y), оканчивающихся в вершине y. p = Head; while (p!=Tail) { x = (*p).Key; DeleteGraph (x,y); p = (*p).Next; } //Удаление списка смежности вершины y. SearchGraph (y, &p); r = (*p).Trail; while (r!=NULL) { s = r; r = (*r).Next; delete s; } //Удаление узла, содержащего вершину y, из списка заголовочных узлов. q = Head; if (q==p) { Head = (*Head).Next; delete q; } else { while ((*q).Next!=p) q = (*q).Next; (*q).Next = (*p).Next; delete p; } }
На следующем шаге мы рассмотрим представление графов с помощью структур Вирта.
