На этом шаге мы рассмотрим модифицированные структуры Вирта.
Часто при реализации алгоритмов на ориентированных графах (см. [1, с.129,143,149]) требуется по заданной конечной вершине некоторой дуги ориентированного графа восстановить список "предшествующих" вершин. Для успешного решения поставленной задачи модифицируем ранее написанные функции MakeGraph(), AddGraph() и PrintGraph() с учетом следующего описания типов:
typedef struct L *Lref; //Тип: указатель на заголовочный узел. typedef struct T *Tref; //Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. int Count1; //Количество последующих вершин. Tref Pred; //Указатель на список смежности, содержащий "предшественников". Tref Trail; //Указатель на список смежности, содержащий "последователей". Lref Next; //Указатель на следующий узел в списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer;
Как и ранее, вершины графа помещаются в связанный список заголовочных узлов, каждый из которых теперь будет содержать шесть полей.
Если указатель P указывает на заголовочный узел, представляющий вершину Q графа, то
- поле (*P).Key содержит информацию, связанную с этой вершиной (идентификатор вершины графа);
- поле (*P).Count содержит количество вершин, "предшествующих" данной;
- поле (*P).Count1 содержит количество вершин, "следующих за" данной;
- поле (*P).Next содержит указатель на заголовочный узел, представляющий следующую вершину графа (если такая вершина есть) в списке заголовочных узлов;
- каждый заголовочный узел является заглавным звеном двух списков узлов второго типа, называемых дуговыми узлами. Такие списки мы, как и ранее, будем называть списками смежности.
Каждый узел списков смежности представляет дугу графа. Поле (*P).Trail указывает на список смежности, представляющий дуги, выходящие из вершины Q графа.
Второй список смежности представляет собой список узлов, представляющих вершины-"предшественники" данной вершины графа. Поле (*P).Pred содержит указатель на этот список.
Каждый узел списков смежности содержит два поля: Id и Next, причем для списка смежности, заданного указателем (*P).Trail, справедливо следующее: если Q указывает на списочный узел, представляющий дугу (A,B), то
- поле (*Q).Id указывает на заголовочный узел, представляющий вершину B графа;
- поле (*Q).Next указывает на списочный узел, представляющий следующую дугу, выходящую из вершины A графа (если такая дуга есть).
На рисунке показан граф и его "улучшенное" представление Вирта:
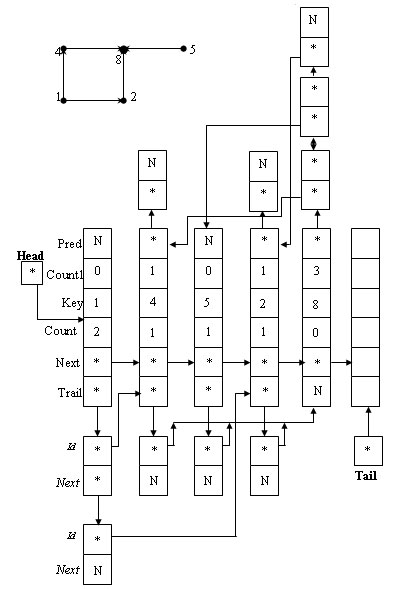
Рис.1. Граф и его улучшенное представление Вирта
Пример. Построение модифицированной структуры Вирта, соответствующей ориентированному графу, вывод ее на экран и добавление ребер.
#include <iostream.h> #define TRUE 1 #define FALSE 0 typedef int Boolean; typedef struct L *Lref; //Тип: указатель на заголовочный узел. typedef struct T *Tref; //Тип: указатель на дуговой узел. //Описание типа заголовочного узла. typedef struct L { int Key; //Имя заголовочного узла. int Count; //Количество предшественников. int Count1; //Количество последующих вершин. Tref Pred; //Указатель на список смежности, содержащий "предшественников". Tref Trail; //Указатель на список смежности, содержащий "последователей". Lref Next; //Указатель на следующий узел в //списке заголовочных узлов. } Leader; //Описание типа дугового узла. typedef struct T { Lref Id; Tref Next; } Trailer; class Spisok { private: Lref Head; //Указатель на список заголовочных узлов. Lref Tail; //Указатель на фиктивный элемент //в конце списка заголовочных узлов. Lref SearchGraph(int); Lref Search(int); public: Spisok () {//Инициализация списка заголовочных узлов. Head = Tail = new (Leader); } ~Spisok(); //Деструктор. void MakeGraph(); void AddGraph(int, int); void DeleteGraph(int, int); void PrintGraph(); void DeleteY(int); void Free1Graph(Lref *, Lref *); void Free2Graph(Tref *); }; void main () { Spisok A; int x,y; //Начало и конец дуги. //Построение и вывод структуры Вирта. A.MakeGraph (); A.PrintGraph (); cout<<endl; cout<< "Добавим к графу новую дугу...\n"; cout<< "Введите начало дуги: "; cin>>x; cout<< "Введите конец дуги: "; cin>>y; A.AddGraph (x,y); A.PrintGraph (); cout<<endl; cout<< "Добавим к графу новое ребро...\n"; cout<< "Введите первую концевую вершину ребра: "; cin>>x; cout<< "Введите вторую концевую вершину ребра: "; cin>>y; A.AddGraph (x,y); A.AddGraph (y,x); A.PrintGraph (); cout<<endl; cout<< "Удалим из графа заданную дугу...\n"; cout<< "Введите начало дуги: "; cin>>x; cout<< "Введите конец дуги: "; cin>>y; A.DeleteGraph (x,y); A.PrintGraph (); cout<<endl; cout<< "Удалим из графа заданное ребро...\n"; cout<< "Введите первую концевую вершину ребра: "; cin>>x; cout<< "Введите вторую концевую вершину ребра: "; cin>>y; A.DeleteGraph (x,y); A.DeleteGraph (y,x); A.PrintGraph (); cout<<endl; cout<< "Введите удаляемую вершину: "; cin>>y; A.DeleteY (y); A.PrintGraph (); cout<<endl; } Spisok::~Spisok() { //Очистка структуры Вирта. Lref t = Head; while (t!=Tail) { Free2Graph (&(*t).Trail); t = (*t).Next; } Free1Graph (&Head,&Tail); delete Tail; } Lref Spisok::SearchGraph (int w) //Функция возвращает указатель на заголовочный узел //с ключом w. Если заголовочный узел отсутствует, то он //добавляется в список. Head - указатель на структуру Вирта. { Lref h; h = Head; (*Tail).Key = w; while ((*h).Key!=w) h = (*h).Next; if (h==Tail) //В списке заголовочных узлов нет узла с ключом w. //Поместим его в конец списка Head. { Tail = new (Leader); (*h).Count = (*h).Count1 = 0; (*h).Trail = (*h).Pred = NULL; (*h).Next = Tail; } return h; } Lref Spisok::Search (int w) //Функция возвращает указатель на заголовочный узел //ключом w. Если узел отсутствует, то функция возвращает NULL . { Lref h = Head; (*Tail).Key = w; //Поиск "с барьером". while ((*h).Key!=w) h = (*h).Next; if (h==Tail) //В списке заголовочных узлов нет узла с ключом w. h = NULL; return h; } void Spisok::MakeGraph () //Функция возвращает указатель Head на модифицированную структуру //Вирта, соответствующую ориентированному графу. { int x,y; Lref p,q; //Рабочие указатели. Tref t,r; // Рабочие указатели. Boolean Res; //Флаг наличия дуги. cout<<"Вводите начальную вершину дуги: "; cin>>x; while (x!=0) { cout<<"Вводите конечную вершину дуги: "; cin>>y; //Определим, существует ли в графе дуга (x,y)? p=SearchGraph (x); q=SearchGraph (y); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) //Если дуга отсутствует, то поместим её в граф. { t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; t = new (Trailer); (*t).Id = p; (*t).Next = (*q).Pred; (*q).Pred = t; (*p).Count1++; } cout<<"Вводите начальную вершину дуги: "; cin>>x; } } void Spisok::AddGraph (int x,int y) //Добавление дуги (x,y) (если ее не было!) к модифицированной структуре //Вирта, соответствующей ориентированному графу Head. { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. //Определим, существует ли в графе дуга (x,y)? p=SearchGraph (x); q=SearchGraph (y); r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (!Res) { //Если дуга отсутствует, то поместим её в граф. t = new (Trailer); (*t).Id = q; (*t).Next = (*p).Trail; (*p).Trail = t; (*q).Count++; t = new (Trailer); (*t).Id = p; (*t).Next = (*q).Pred; (*q).Pred = t; (*p).Count1++; } } void Spisok::DeleteGraph (int x,int y) //Функция возвращает указатель Head на структуру //Вирта, соответствующую ориентированному графу //и полученную удалением дуги (x,y). { Lref p,q; //Рабочие указатели. Tref t,r; //Рабочие указатели. Boolean Res; //Флаг наличия в графе данной дуги. //Определим, существует ли в графе дуга (x,y)? p=Search (x); q= Search (y); if ((p!=NULL)&&(q!=NULL)) { //Вершины x и y в графе есть. r = (*p).Trail; Res = FALSE; while ((r!=NULL)&&(!Res)) if ((*r).Id==q) Res = TRUE; else r = (*r).Next; if (Res) //Если дуга существует, то удалим её. if (r==(*p).Trail) { (*p).Trail = (*(*p).Trail).Next; delete r; (*q).Count--; } else { t = (*p).Trail; while ((*t).Next!=r) t = (*t).Next; (*t).Next = (*(*t).Next).Next; delete r; (*q).Count--; } } } void Spisok::PrintGraph () //Вывод модифицированной структуры Вирта, заданной указателем //Head и соответствующей ориентированному графу. { Lref p; //Рабочий указатель. Tref q; //Рабочий указатель. p = Head; while (p!=Tail) { cout<<(*p).Key<<"(("; q = (*p).Trail; while (q!=NULL) { cout<<(*(*q).Id).Key<<" "; q = (*q).Next; } cout<<")("; q = p->Pred; while (q!=NULL) { cout <<(*(*q).Id).Key<<" "; q = q->Next; } cout<<"))"; p = (*p).Next; cout<<" "; } } void Spisok::DeleteY (int y) //Функция возвращает указатель Head на структуру Вирта, //соответствующую графу с удаленной вершиной y. { Lref p,q; //Рабочие указатели. Tref r,s; //Рабочие указатели. int x; //Рабочая переменная. //Удаление всех дуг (x,y), оканчивающихся в вершине y. p = Head; while (p!=Tail) { x = (*p).Key; DeleteGraph (x,y); p = (*p).Next; } //Удаление списка смежности вершины y. p=SearchGraph (y); r = (*p).Trail; while (r!=NULL) { s = r; r = (*r).Next; (*(*s).Id).Count++; delete s; } //Удаление узла, содержащего вершину y, из списка заголовочных узлов. q = Head; if (q==p) { Head = (*Head).Next; delete q; } else { while ((*q).Next!=p) q = (*q).Next; (*q).Next = (*p).Next; delete p; } } void Spisok::Free1Graph (Lref *Head, Lref *Tail) //Очистка динамической памяти, занятой линейным списком, // заданным указателем *Head. { if (*Head!=*Tail) { Free1Graph (&(**Head).Next,Tail); delete *Head; *Head = NULL; } } void Spisok::Free2Graph (Tref *X) //Очистка динамической памяти, занятой линейным списком, // заданным указателем *X. { if (*X!=NULL) { Free2Graph (&(**X).Next); delete *X; *X = NULL; } }
Замечание. Вы должны представлять важное различие между представлениями графа в виде матрицы смежностей и представлениями в виде структур смежности [2, с.408].
Если граф представлен с помощью матрицы смежностей, то у нас появляется возможность очевидного прохождения по строке или столбцу матрицы. Просмотр строки эквивалентен нахождению всех дуг, выходящих из данной вершины, что может быть эффективно реализовано при связанном представлении путем прохождения списка всех дуговых узлов, начинающегося с данного заголовочного узла.
Однако просмотр столбца матрицы смежностей эквивалентен нахождению всех дуг, оканчивающихся в данном узле, а для этой процедуры нет соответствующего простого метода для связанного представления, если не воспользоваться модифицированной структурой Вирта.
Конечно, Вы должны выбрать из этих представлений наиболее подходящее, исходя из требований конкретной задачи с учетом эффективности использования памяти и минимизации времени исполнения.
(1) Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.
(2) Лэнгсам Й., Огенстейн М., Тененбаум А. Структуры данных для персональных ЭВМ: Пер. с англ. - М.: Мир, 1989. - 568 с.
На следующем шаге мы познакомимся с представлением отношений.
